MB
Size: a a a
2020 September 16
Это для той трактовки условия, в которой все знаки должны быть строго положительны или строго отрицательны.
MB
Тогда может случиться, например, что пересечение есть, но это отрезок. Тогда ответ NO.
Ш
Это для той трактовки условия, в которой все знаки должны быть строго положительны или строго отрицательны.
спасибо)
A

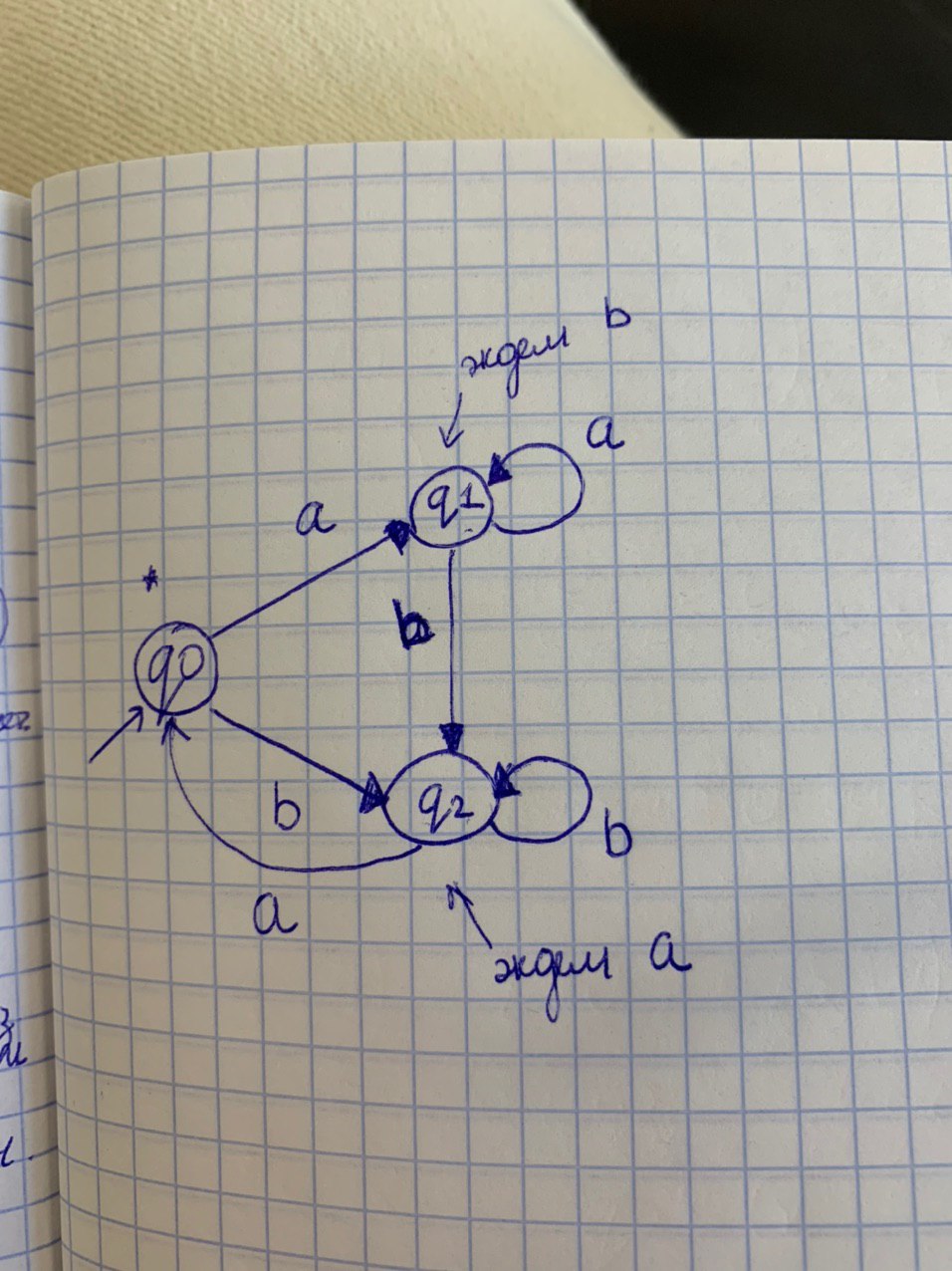
Привет)) кто-нибудь может помочь построить детерминированный конечный автомат по такому выражению?(схему)
A
ну как. Стартовое состояние. Если нашли a, то идем в состояние "ждем b", если b, то в состояние "ждем a", иначе успех. Состояние "ждем a" - если a, то к началу, иначе откатить последний символ и успех. Для "ждем b" аналогично
A
Как откатить?
A
Если правильно поняла
A
A
нет, q1 и q2 симметричны и между ними нет перехода
A
плюс нужен "выход"
A
То есть я строю автомат у которого количество b и a должно быть одинаковым
A
не совсем так, они должны идти парами. Если сначала пришло a, то следующее должно быть b. И наоборот
A
A
попадание любого другого символа означает выход из этого автомата
A
нет, петель там быть не должно
A
aa не является валидным для этого выражения
A
abba - является. abb нет.
A
Ещё одно состояние должно быть?
A
я не знаю, каким именно образом это регулярное выражение должно применяться
A
если мы говорим про конечную машину регулярного выражения, то у нас на выходе два состояния - либо есть соответствие выражению, либо нет соответствия выражению.