ВВ
Size: a a a
2020 September 15
А зачем потребовалось считать факториал? Обычно от прямого вычисления удаётся так или иначе избавиться.
IB
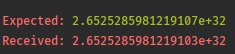
Прошу прощения за странный вопрос, но почему может быть такое поведение? Факториал обычный
А в каком порядке умеожаешь? Хотя все равно будет потеря точности рано или поздно.
ПК
для целых чисел такого размера лучше брать библиотеки длинной арифметики
Есть bc из таких
AS
А зачем потребовалось считать факториал? Обычно от прямого вычисления удаётся так или иначе избавиться.
Для обучения, не более
A(
Для обучения, не более
в таком случае не имеет значения аутпут в 18 знаке
A(
может для задачи?
ПК
Ну считать число сочетаний можно аккуратно
ПК
Во что переименуют красно-чёрные деревья?
@N
Во что переименуют красно-чёрные деревья?
В красно-афромериканские
BV
В красно-афромериканские
в мажоритарно-миноритарные
P
Во что переименуют красно-чёрные деревья?
В инклюзивно-дайверсные
D
В инклюзивно-дайверсные
Вот это хорошо было
MB
Во что переименуют красно-чёрные деревья?
В альфа-бета
2020 September 16
Ш
Привет всем, если у нас есть n прямых вида A_i * x + B_i * y + C_i = 0 как проверить что для всех этих n прямых существует такая точка (x, y) что если подставить их то знак у всех A_i * x + B_i * y + C_i будет одинаковый ? )
Ш
n <= 100
MB
Привет всем, если у нас есть n прямых вида A_i * x + B_i * y + C_i = 0 как проверить что для всех этих n прямых существует такая точка (x, y) что если подставить их то знак у всех A_i * x + B_i * y + C_i будет одинаковый ? )
Каждая прямая задает полуплоскость. Рассмотрим пересечение этих полуплоскостей.
В зависимости от определения понятия "знак" тебя либо просят проверить, что пересечение не пусто, либо просят проверить, что в нем есть внутренняя точка (то есть его площадь больше 0).
В зависимости от определения понятия "знак" тебя либо просят проверить, что пересечение не пусто, либо просят проверить, что в нем есть внутренняя точка (то есть его площадь больше 0).
Ш
Привет всем, если у нас есть n прямых вида A_i * x + B_i * y + C_i = 0 как проверить что для всех этих n прямых существует такая точка (x, y) что если подставить их то знак у всех A_i * x + B_i * y + C_i будет одинаковый ? )
Кстати забыл сказать что x, y должны быть положительными
MB
В таких ограничениях задача нестрашная: можно попарно пересечь все прямые, получится некоторый набор точек. Далее из них нужно выбрать те, которые принадлежат каждой из полуплоскостей.
Дальнейшие действия зависят от того, что именно от тебя просят.
В одном случае надо просто проверить, что хотя бы одна такая точка существует.
В другом надо проверить, что какие-то три хорошие точки не лежат на одной прямой.
Дальнейшие действия зависят от того, что именно от тебя просят.
В одном случае надо просто проверить, что хотя бы одна такая точка существует.
В другом надо проверить, что какие-то три хорошие точки не лежат на одной прямой.
MB
Ах да. На самом деле этот алгоритм надо два раза запустить. Один раз для каждой прямой выбрать положительную плоскость, в другой раз отрицательную.
Ш
а я вот не понял зачем "В другом надо проверить, что какие-то три хорошие точки не лежат на одной прямой."



