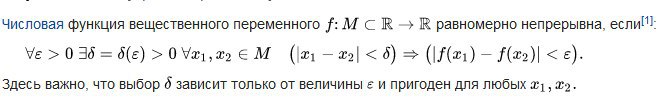ВМ
собственно, на википедии всё объяснено же
Или статью эту не видел. Поищу.. Спасибо
Size: a a a
2020 January 07
V
Вот Такой Молодой Человек
Я не вкатил..
вкатил в обычное определение непрерывности?
V
как там связаны эпсилон и дельта
ВМ
Да, я понимаю, о чем эти два определения, я понимаю и могу воспроизвести док-во теоремы Кантора, но остаётся туманной существенная разница между ними..
V
непрерывность обычная - это локальное свойство. Она говорит, что функция в точке непрерывна, если ограничив разность аргументов функции эпсилоном, ты ограничишь разность значений функций дельтой
V
а непрерывность равномерная - это глобальное свойство, не локальное
ВМ
Ну локальное - то есть непрерывность в точке?
V
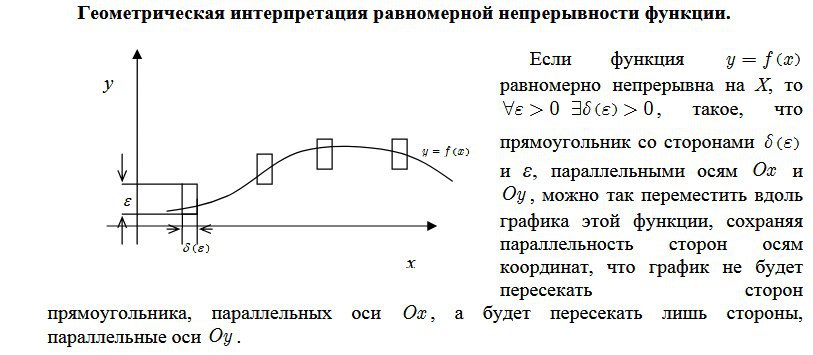
она говорит, что для любого эпсилона существует дельта, притом одна для любой точки отрезка
V
то есть ты одной дельтой ограничиваешь разность значений функций сразу на отрезке
ВМ
Сори, я просто гуманитарий, потерявшийся на теормехе
V
V
вот
V
пишут, что дельта зависит только от эпсилона, но не от выбора точки
ВМ
Да, это определение, но в чем прикладная разница между ними. Вопрос, скорее, в этом
V
V
ну вот функция 1/x
V
она непрерывна
ВМ
Да
V
но не равномерно непрерывна
V
потому что у неё в нуле фигня