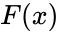Короче, если убрать воду, то — библиотеки может, и будут, но вот 100% гарантии их работы на любых функциях никто не даст

Ну, топорненький инструмент под задачу за время, прошедшее с задания вопроса, можно было уже написать

И понять, что

Потому что даже задача локализации корня — та ещё задача

можно сразу вспомнить ф-ю Вейерштрассе :)

Она не гладкая

ну в этом и смысл :)

Ну я тип к тому, что можно ограничить условиями до каких то разрешаемых случаев. На практике достаточно будет иметь  рандом член, вида которого ты не знаешь, чтобы была вероятность засесть на недельку, и ниче не решить.

sin(1/x)

я просто хотел показать ему функцию, которая определена везде, гладкая везде, и при этом для любого целого N и сколь угодно малого epsilon>0 найдётся участок (x, x+epsilon), на котором у функции будет не меньше N корней :)

Привет

О, привет

Как будто это проблема

Всем привет. Есть кто в Scilab разбирается ?

Ребят, а я не могу понять, нужно ли рассматривать в факторизации Кронекера отрицательные делители?
Может, кто-то подсказать?

https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%9A%D1%80%D0%BE%D0%BD%D0%B5%D0%BA%D0%B5%D1%80%D0%B0

Есть функция f(X) = Y, где X это набор из трех значений (x1, x2, x3), а Y это (y1,y2). На самом деле y1 = g(x1,x2,x3), и y2 = h(x1,x2,x3, y1). y1 — это набор из ограниченного количества значений (дискретная область значений). Функции h и g — "дорогие" в вычислении, поэтому я вычисляю значения подставляя х1, х2, х3 по сетке с определенным шагом, а остальные значения хочу интерполировать. Вопрос: какие есть методы, как лучше гуглить, чтобы разобраться в этой теме?

Линейные, квадратичные, кубические интерполяции, сплайны