T
Size: a a a
2020 January 09
T
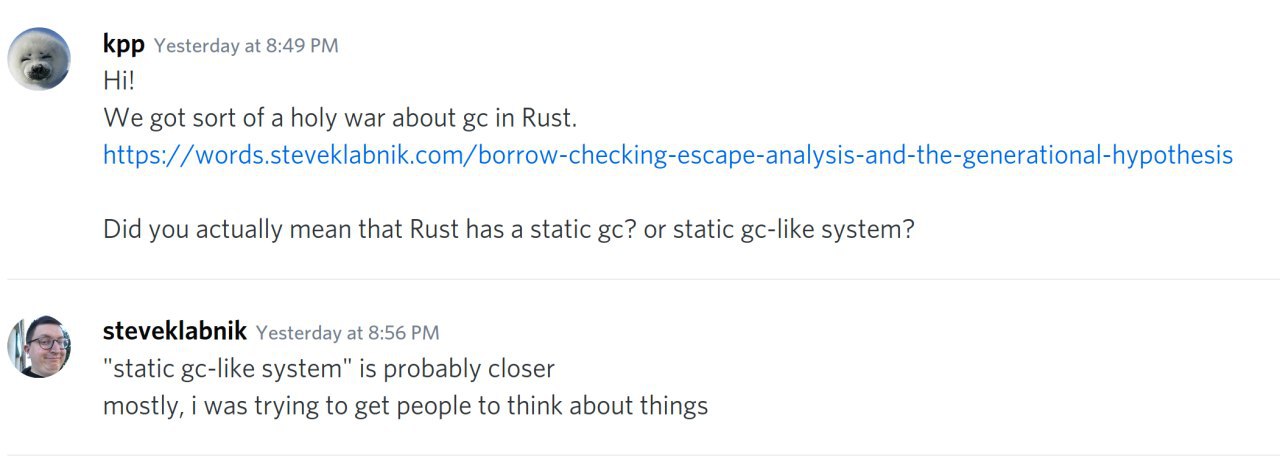
тесты это как типы, только хуже
я сейчас прямо пытаюсь применить теорию типов к тестированию.
уже полгода вожусь
уже полгода вожусь
T
тесты это как типы, только хуже
ты думаешь что пошутил
T
я думал, что это оригинальная свежая идея -_-
ML
Шикарно!
+
ML
Так что без осознанного плана броуновское движение людей будет просто бесполезно греть атмосферу и просирать ни в чём не повинные конечные ресурсы.
Я-таки считаю, нам нужен осознаваемый всеми и правильный план, который будет объединять людей. Пока люди друг друга херачат за ресурсы, экономически и физически.
(это к цитате чуть выше ^^^)
Я-таки считаю, нам нужен осознаваемый всеми и правильный план, который будет объединять людей. Пока люди друг друга херачат за ресурсы, экономически и физически.
(это к цитате чуть выше ^^^)
Spot the commie
AZ
You may think of functors as generalized containers for storing arbitrary types of values. You can imagine that they have shapes; and for two containers of the same shape you may establish a correspondence between “positions” at which the elements are stored. This is quite easy for traditional containers like lists or trees, and with a leap of faith it can be stretched to non-traditional “containers” like functions. We used the intuition of relations corresponding to the idea of “occupying the same position” within a data structure. This notion can be readily generalized to any polymorphic containers. Two trees, for instance, are related if they are both empty, or if they have the same shape and their corresponding elements are related.
AZ
посмеялся с with a leap of faith it can be stretched to non-traditional “containers” like functions
AZ
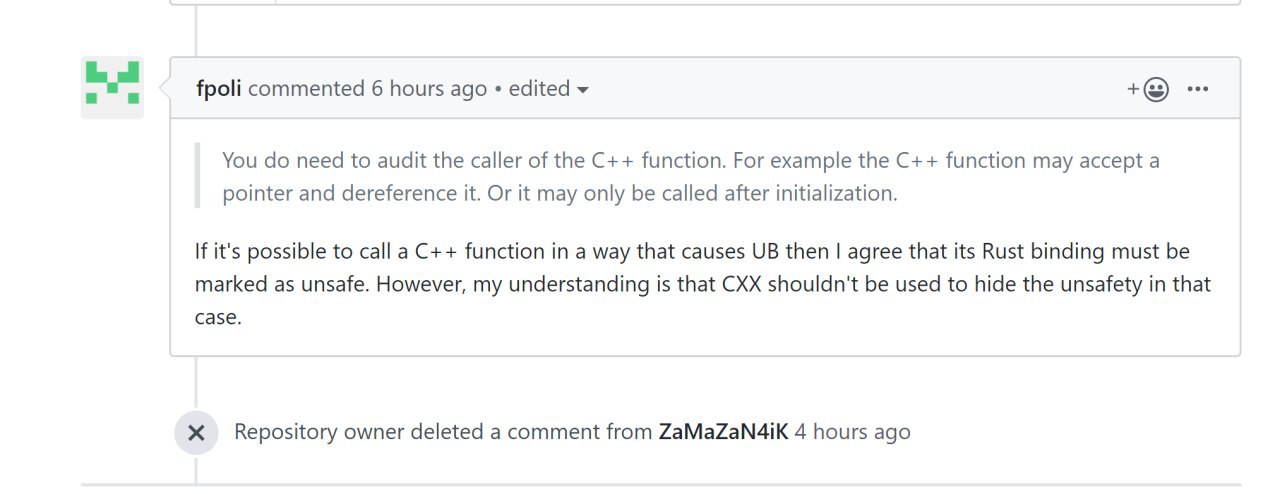
Чет мне захотелось увидеть тот коммент
DF
В математике есть раздел где функция ето вектор
DF
Но здесь по моему что то иное имеется в виду
DF
Потому что он употребляет слово related
2020 January 10
AZ
речь про то что функция это функтор
AZ
OA
people don't want to think
OA
they want to argue about terminology
DF
А Клабник етот большой человек в расте?
OA
самый главный