При обучении всё это распределяется по кластеру TPUv4 (для самой большой модели использовались 1024 TPU чипа), эксперты с одинаковыми индексами в разных слоях живут на одних и тех же устройствах, чтобы граф вычислений был одинаковым для каждого MoE слоя. В шардинге полагаются на компилятор GSPMD (https://arxiv.org/abs/2105.04663). Используется дополнительный MoE loss из работы про GShard, чтобы более равномерно раскидывались токены по экспертам. Авторы добились стабильного обучения сетей разного размера с одним набором гиперпараметров.

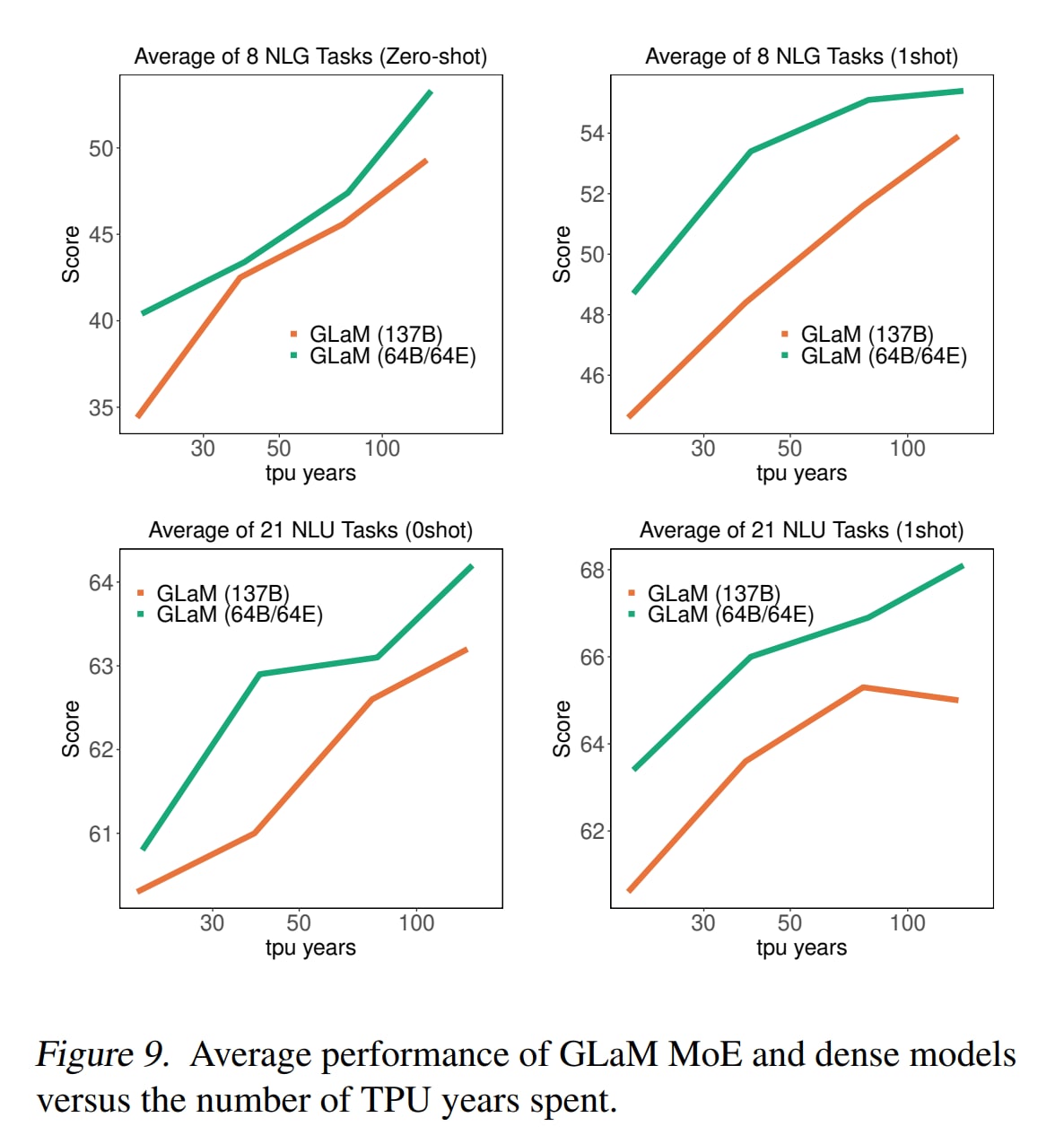
Для оценки моделей отобрали 29 датасетов (8 для задач NLG, 21 для NLU). Это оригинальный набор из 42 датасетов, на котором оценивали GPT-3 (https://t.me/gonzo_ML/305), с отброшенными 7 синтетическими задачами на арифметику и т.п., а также 6 датасетами для машинного перевода. Сравнивают на zero-shot и one-shot.

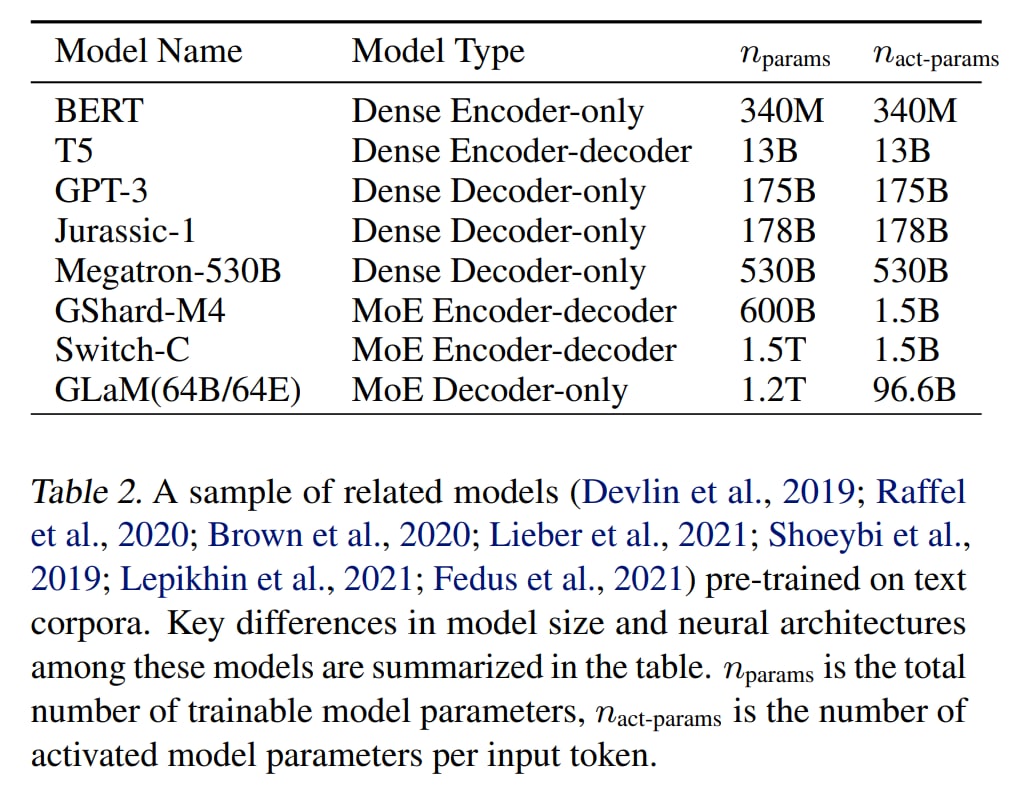
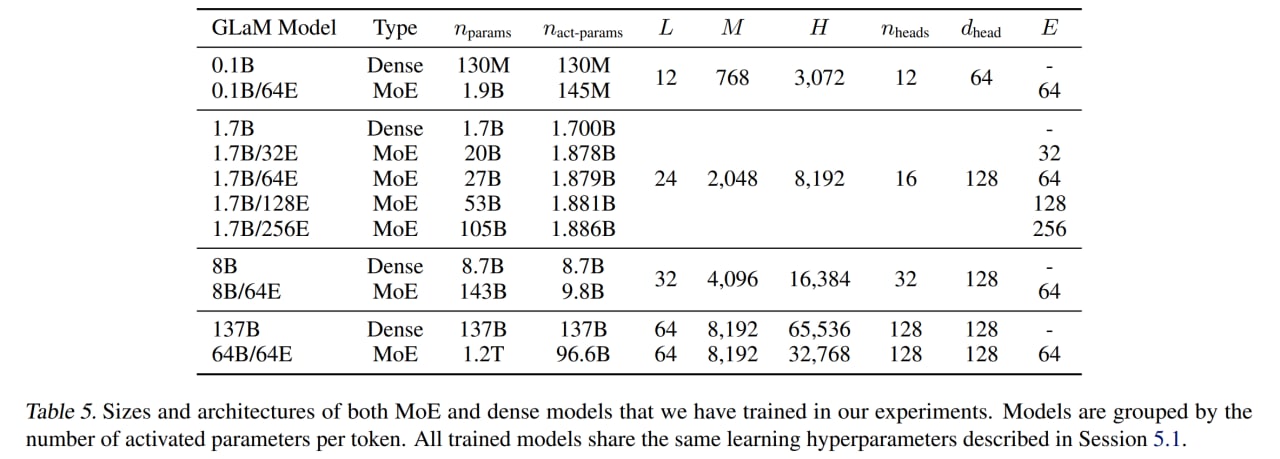
Сравнивают разные модели с упором на одинаковое количество вычислений или количество активных параметров на токен.

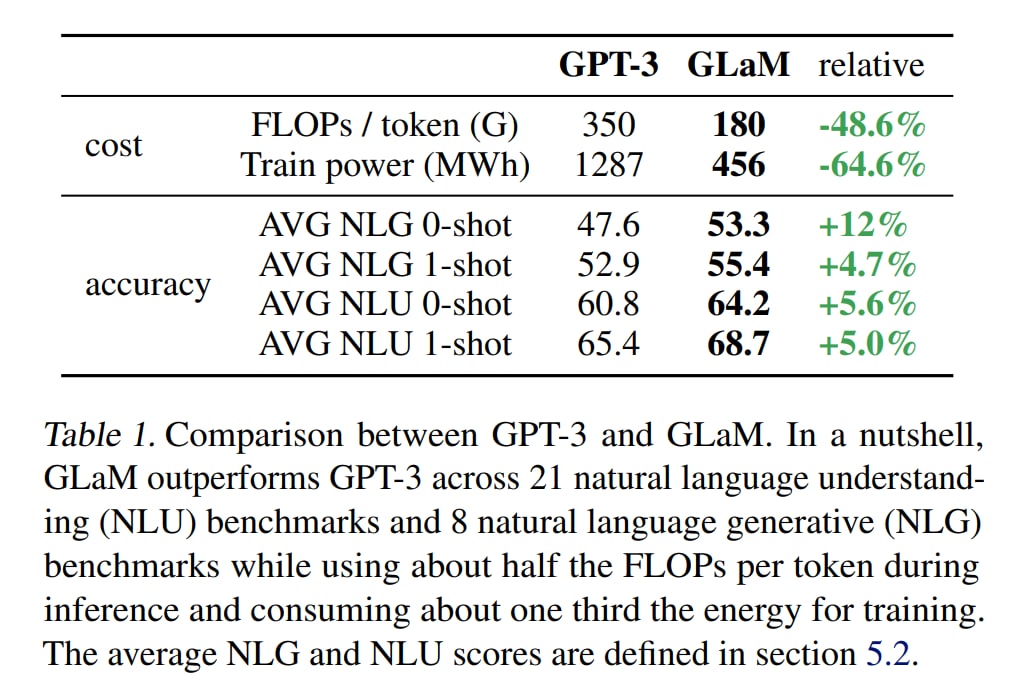
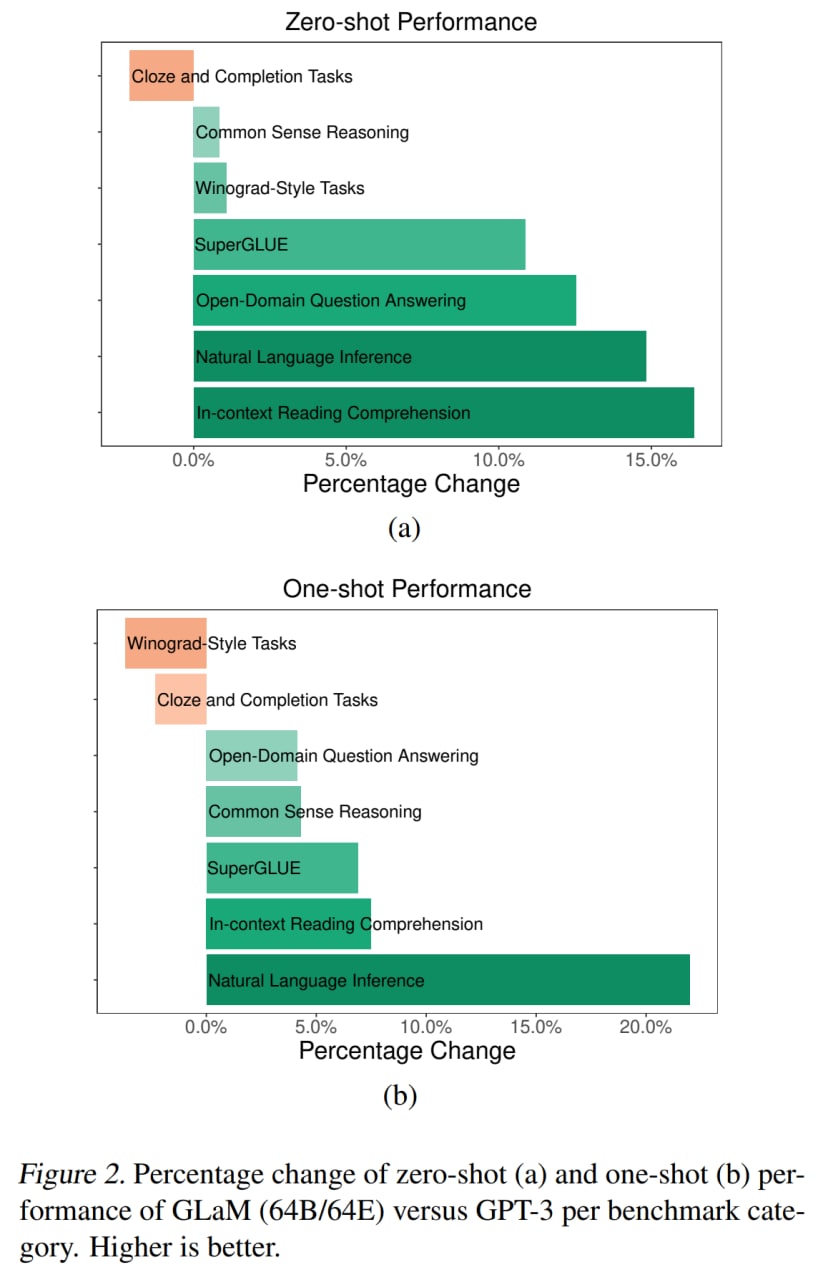
В целом по 5 из 7 категорий задач GLaM заметно превзошла GPT-3. При этом GLaM 64B/64E (самая большая) с 96.6B активных весов на токен (у самой большой GPT-3 их 175B) во время инференса требует примерно в два раза меньше вычислений для того же входа.

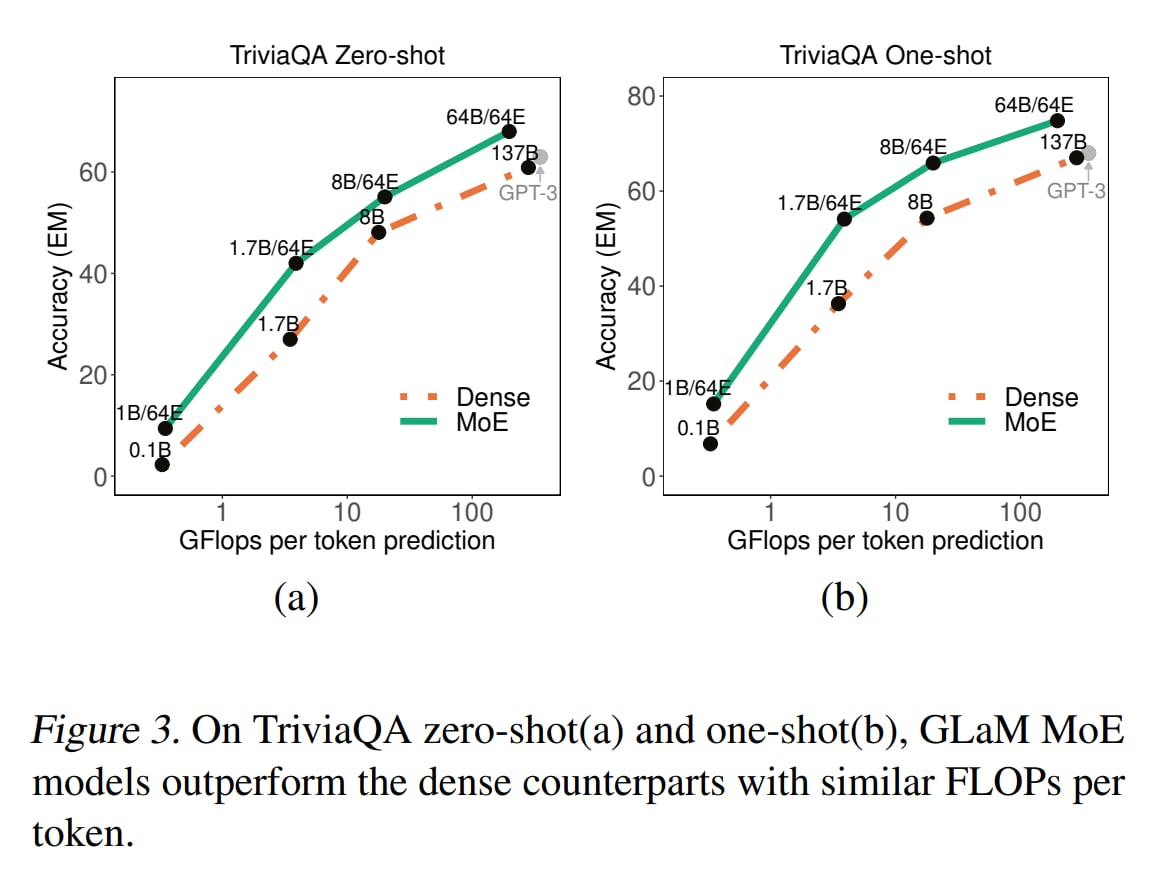
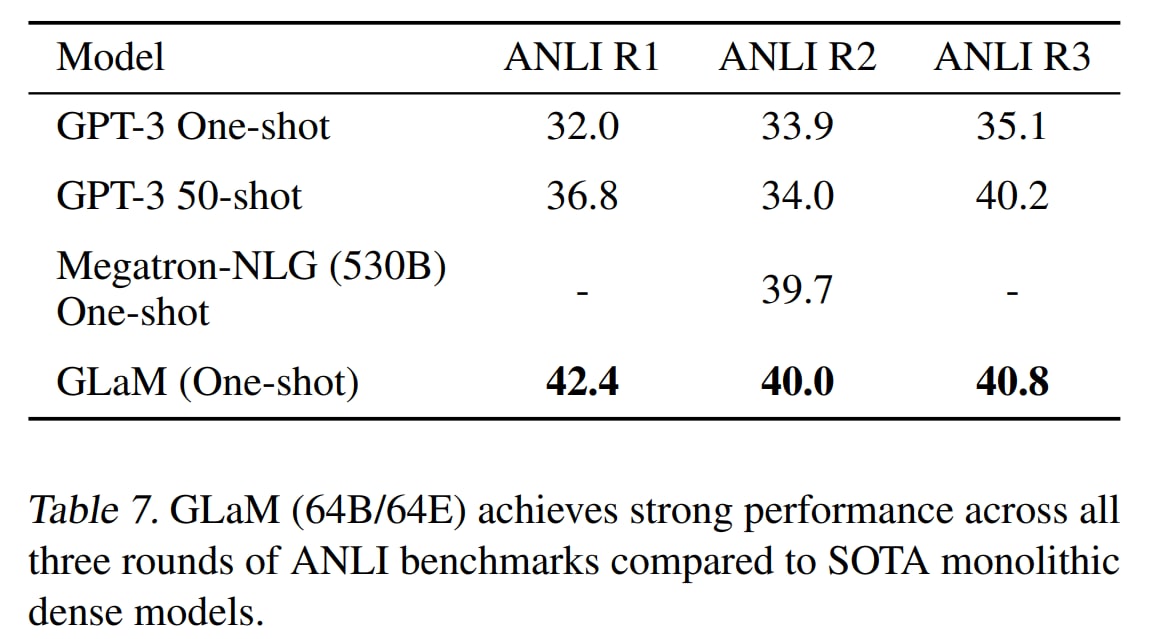
На TriviaQA побили старую SoTA. На ANLI дают качество выше, чем у Megatron-NLG с 530B параметров, при этом требуя менее 20% вычислений последнего.

Авторы также поисследовали bias’ы модели, показали, что она установила SoTA на WinoGender, превзойдя GPT-3.

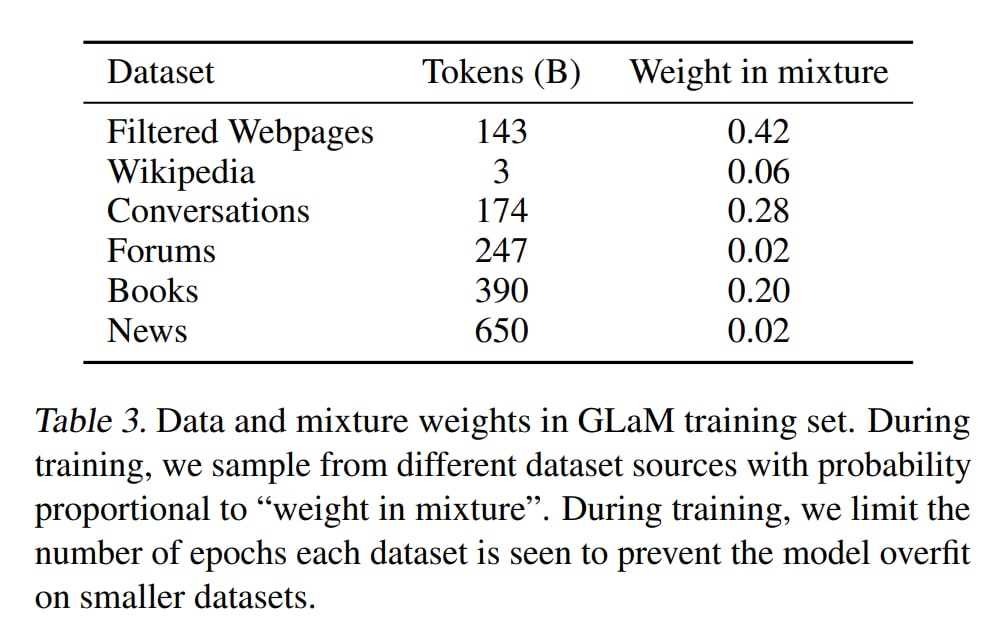
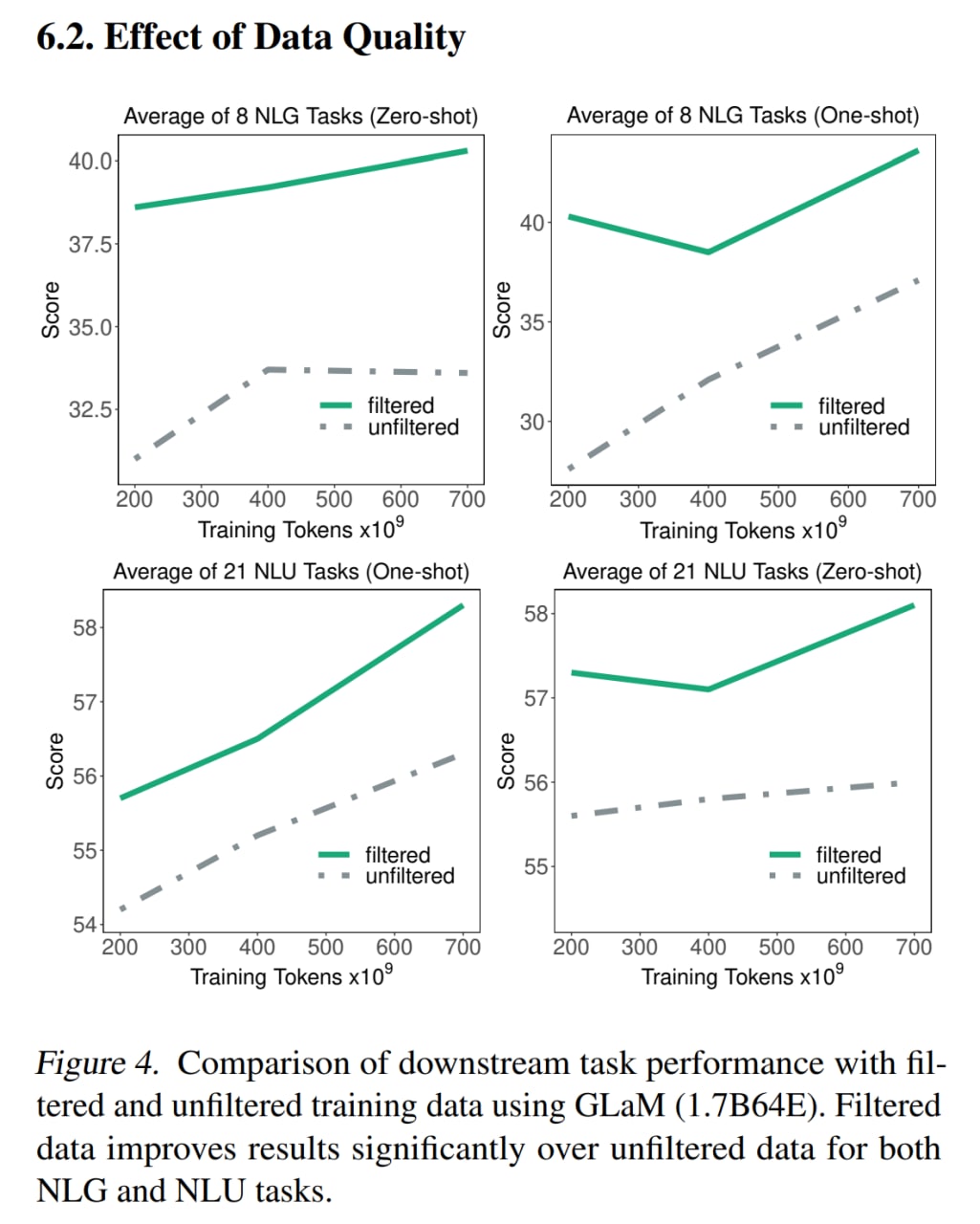
Отдельно померяли влияние качества данных, показали, что более качественные фильтрованные данные крайне важны, объёмом до этих цифр так просто не доберёшь.

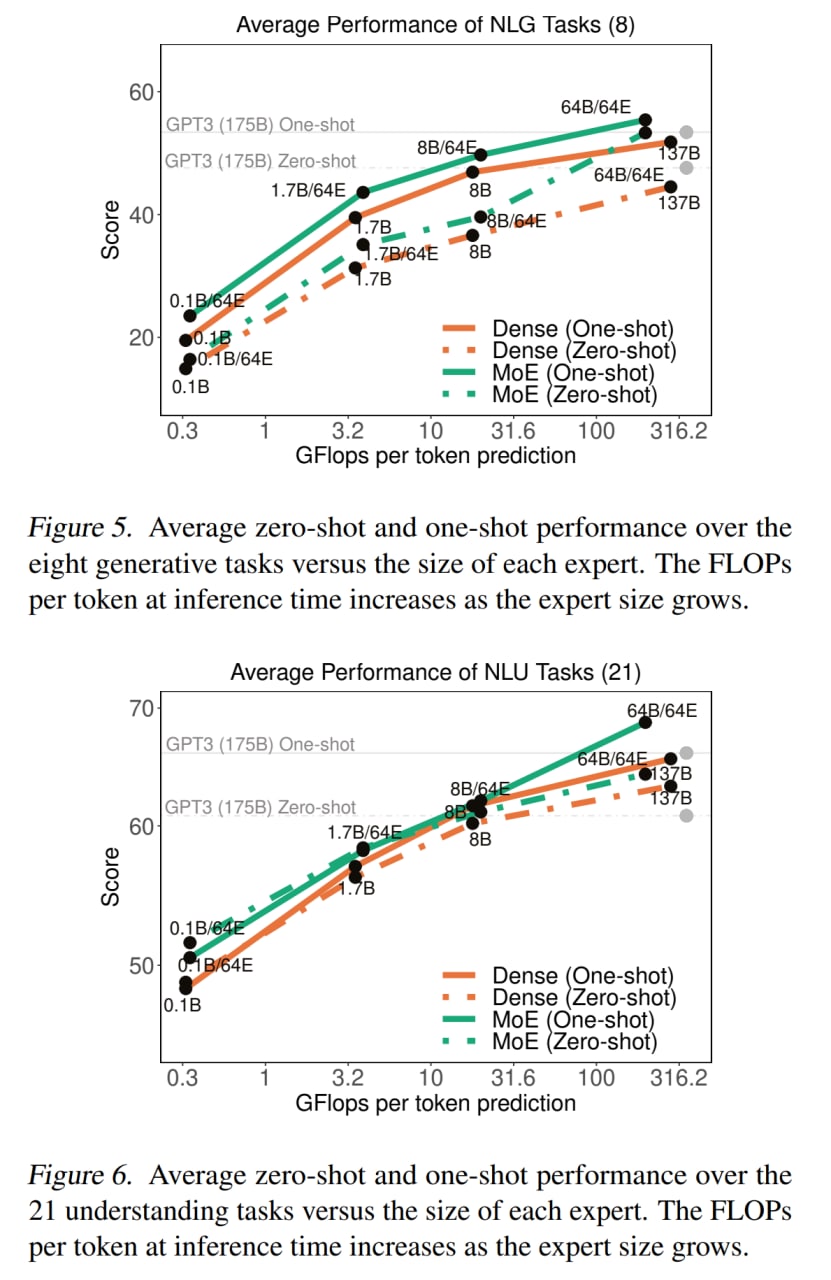
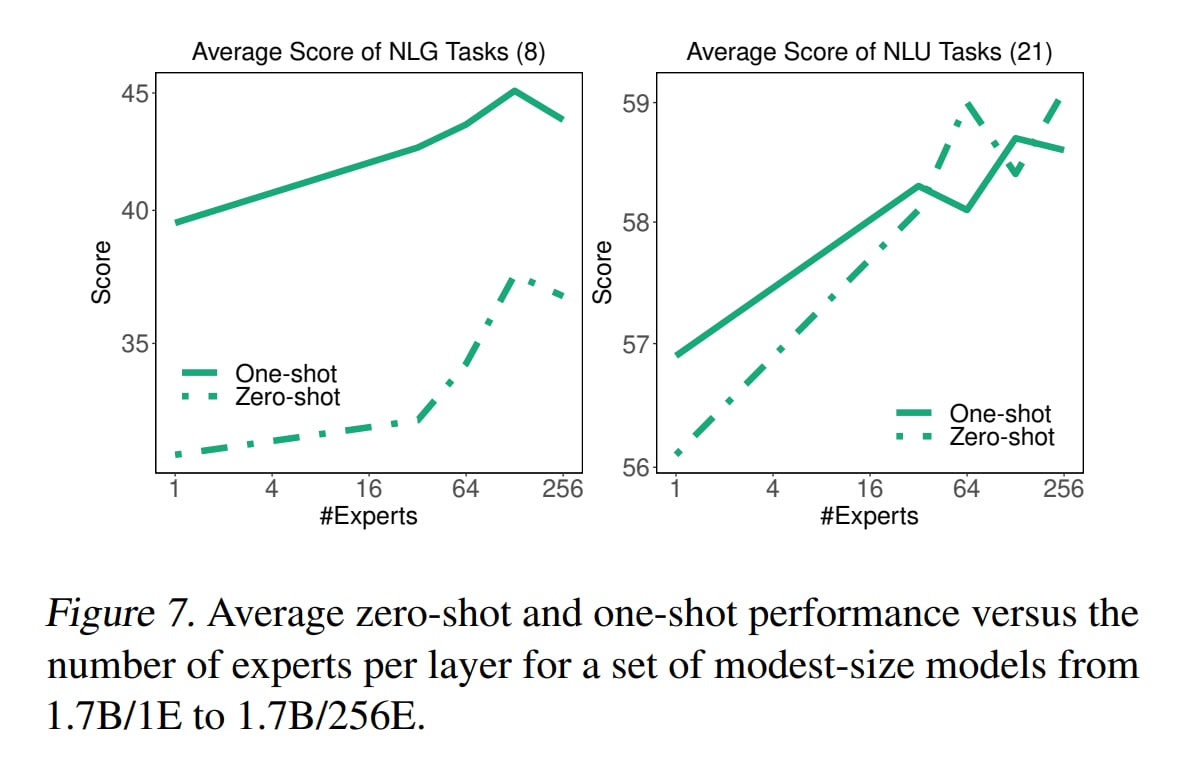
И с ростом сети (и соответственно ростом размера отдельного эксперта), и с ростом числа экспертов, качество увеличивается.

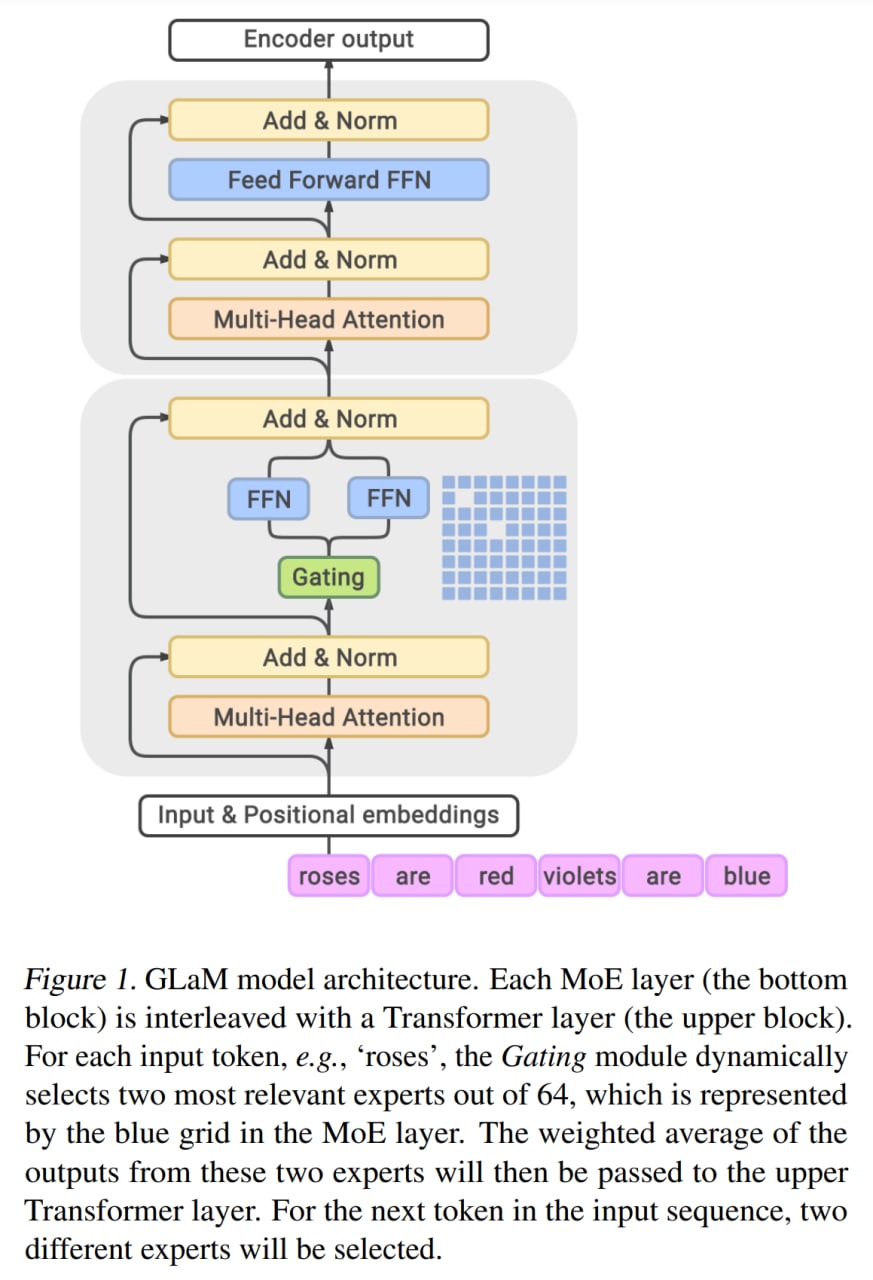
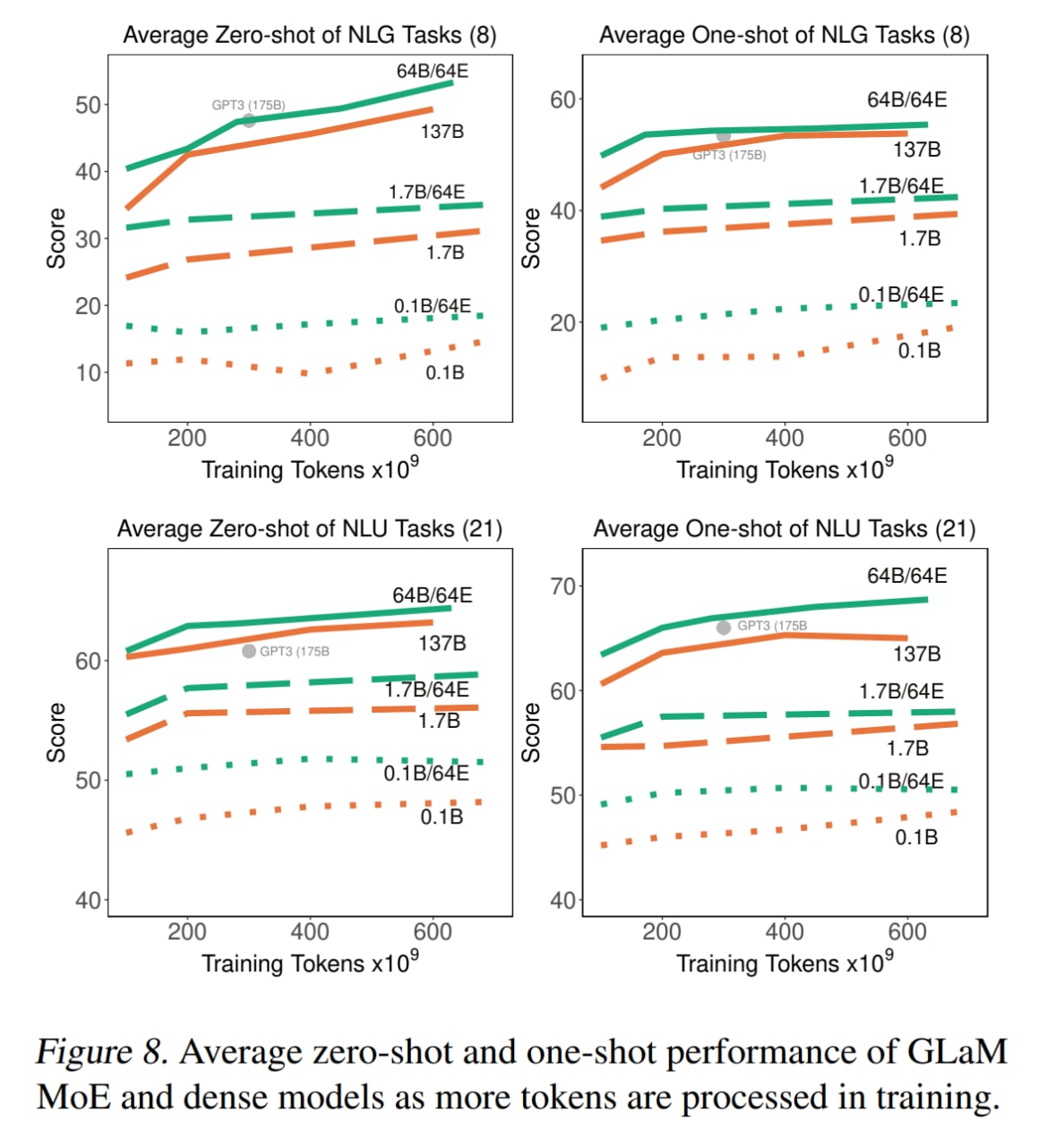
По сравнению с dense моделями у MoE видны два преимущества.

Во-первых, MoE оказываются более эффективны по данным — им требуется меньше данных, чем плотным моделям с сопоставимыми вычислительными требованиями, чтобы достичь сравнимого перформанса на zero-shot/one-shot.

Во-вторых, по количеству вычислений и потребляемой энергии MoE эффективнее плотных сетей. А если сравниваться с GPT-3, то самый большой GLaM потребовал примерно ⅓ энергии от обучения GPT-3.

Правда, тут же мы сравниваем обучение GPT-3 на GPU, которыми были V100, и GLaM на TPUv4, что сильно разное. По цифрам у железа вроде разница не безумная: у одного чипа TPUv3 было что-то в районе 120 TFLOPS/450 Вт, у TPUv4 грубо в районе 250 TFLOPS на фиг знает сколько ватт, возможно 450-500, у V100 было в районе 125 TFLOPS/300 Вт для тензорных ядер и FP16, у A100 было бы 312 TFLOPS/300-400 Вт. Тут конечно много дьявола в деталях, да и на пиковые значения плохо ориентироваться, но разница в железе кажется тоже должна была повлиять и не особо корректно всю разницу в потреблении приписывать архитектуре MoE.

Ещё из любопытных цифр на злобу дня — это carbon emissions. Полное обучение GLaM на 600B токенов оценено в 456 МВт*ч и 40.2 тонны выбросов CO2. Для GPT-3 приводятся цифры в 1297 МВт*ч (в другой таблице 1287, что кажется более правильно и соответствует другому источнику — https://arxiv.org/abs/2104.10350) и 552 тонны CO2. Для сравнения, в статье Паттерсона по упомянутой только что ссылке полёт целого самолёта в обе стороны SFO-JFK даёт в среднем 180.4 тонн. На этом фоне всё же и GPT-3 выглядела не так страшно (ну да, целых 3 таких полёта, что мне кажется несопоставимо с пользой модели), а GLaM так вообще круто.

Жаль вот только, модель не опубликована и будет ли как-то доступна, неясно.

Long Expressive Memory for Sequence Modeling
T. Konstantin Rusch, Siddhartha Mishra, N. Benjamin Erichson, Michael W. Mahoney
Статья: https://arxiv.org/abs/2110.04744
Код: https://github.com/tk-rusch/LEM

Нельзя было пройти мимо модели под названием LEM.

Мы старались писать про многое за пределами трансформеров — и про свёрточные, и про возвращение старых добрых MLP, но что-то давно не писали про рекуррентные сети. А там жизнь тоже идёт ого-го!

Может показаться, что трансформеры вытеснили рекуррентные сети отовсюду, где надо было работать с последовательностями. Но ощущение это ложное. Если посмотреть на некоторые бенчмарки про работу с последовательностями на PapersWithCode, то в топе там либо разные варианты рекуррентных сетей (посимвольное языковое моделирование на Penn Treebank или PoS-тэггинг там же, https://paperswithcode.com/sota/language-modelling-on-penn-treebank-character и https://paperswithcode.com/sota/part-of-speech-tagging-on-penn-treebank), либо варианты хитрых свёрток или гибриды с ними (различные варианты time-series бенчмарков https://paperswithcode.com/task/time-series-classification или sequential mnist https://paperswithcode.com/sota/sequential-image-classification-on-sequential).

Рекуррентные сети для многих по привычке заканчиваются на LSTM/GRU, но кроме этих уже довольно старых моделей за прошедшие годы в области случилось много чего. Может у кого-то на слуху AWD-LSTM или Mogrifier, но это всё равно далеко не полная картина, новые модели появляются каждый год. LEM (Long Expressive Memory) одна из таких моделей, появившаяся в конце 2021 года.

Традиционно считается, что существенная часть проблем при обучении рекуррентных сетей происходит из-за затухающих/взрывающихся градиентов. Собственно, LSTM и GRU были сделаны для борьбы с этим, там за счёт системы гейтов модель учится управлять градиентами так, чтобы они не терялись. Другой подход в этому же снаряду заключается в добавлении специальных ограничений на структуру весов скрытого слоя, например, чтобы матрицы весов были ортогональными или унитарными. Сюда относятся, например, uRNN (https://arxiv.org/abs/1511.06464) или nnRNN (https://arxiv.org/abs/1905.12080). Ещё один подход регулирует веса или структуру, чтобы градиенты оставались вменяемыми. Так поступают в IndRNN (https://arxiv.org/abs/1803.04831) или в более хитрой гарантирующей ограниченность градиентов coRNN (https://arxiv.org/abs/2010.00951) от тех же авторов, что и LEM. Главное, чего хочется добиться кроме отсутствия проблем с обучением, это сохранить выразительность сети и способность выучивать сложные функции.

Авторы отталкиваются от наблюдения, что реалистичные последовательности данных содержат информацию на разных масштабах (например, временных), и соответственно нужна модель способная работать на этих нескольких масштабах (multiscale model).

Начинают рассмотрение с системы из двух обыкновенных дифференциальных уравнений (ODE) с двумя разными масштабами времени (условно, медленный и быстрый). У модели соответственно есть быстрая и медленная переменные y(t) и z(t) и входной сигнал u(t). Размерности всех переменных для простоты одинаковы. Есть и матрицы весов W_y, W_z, V_y, V_z, задающие взаимодействие между нейронами.

Двух масштабов может быть недостаточно для реальных данных, поэтому авторы обобщают систему уравнений до мультимасштабной версии, где константы масштабов заменяются на обучаемые функции похожего на функции исходной системы вида (только с нелинейностью в виде сигмоиды вместо гиперболического тангенса), которые далее поэлементно перемножаются с оригинальными уравнениями. Получаются обучаемые масштабы, которые ещё и адаптивно подстраиваются под данные.

Как бонус эта мультимасштабная система получается той же формы, что и старая добрая модель Ходжкина-Хаксли.

Для того, чтобы перейти к конкретному алгоритму, фиксируют некоторый Δt, систему дискретизуют и получают LEM с двумя скрытыми состояниями y, z (которые можно поставить в соответствие скрытому состоянию ‘h’ и состоянию ячейки ‘c’ для LSTM соответственно) и входом u. К ячейке добавляют линейное выходное состояние, получаемое из y.

Отдельно авторы показывают, что выбирая специальные значения в качестве гейтов и Δt, а также реализовав упомянутое выше соответствие скрытых состояний, LEM можно свести к LSTM. Но важно, что это соответствие есть только при очень жёстких предположениях.

Далее авторы анализируют полученную модель и показывают, что скрытые состояния ограничены, градиенты тоже ограничены, проблема затухающих градиентов устраняется. Доказывают, что LEM может приближать очень большой класс динамических систем и мультимасштабные динамические системы.

Эмпирически проверили на нескольких задачах.

В задаче очень длинного сложения на вход модели поступает двухмерная последовательность размера N*2, где по длинному измерению случайные числа, а по короткому — нули кроме двух позиций в разных половинах последовательности, тут стоят единицы. На выходе надо дать сумму двух чисел, стоящих напротив единиц. Проверяли на N=2000, 5000 и 10000. LEM рулит и сходится быстрее других продвинутых моделей.

На sequential MNIST (sMNIST), когда картинки MNIST’а растягиваются в длинный вектор и подаются пиксель за пикселем, и на permuted sequential MNIST (psMNIST), когда они ещё и случайно перемешиваются (все с одной фиксированной перестановкой), а также на noisy CIFAR-10 (nCIFAR-10), когда картинки построчно схлопываются по каналам и отправляются как 96-мерные последовательности длины 32 и к которым после первых 32 входов (осмысленных) добавляется пэддинг случайным шумом до размера последовательности 1000. То есть модели надо не просто классифицировать картинку, а ещё не забыть ценную информацию после кучи шумовых входов. LEM снова рулит.

На задаче EigenWorms (http://www.timeseriesclassification.com/description.php?Dataset=EigenWorms) надо классифицировать нематоду по нескольким классам (wild type и 4 мутанта) по данным о движении червяка. Каждая последовательность длины 17984, всего таких 259. Трансформер на таком обучать, кажется, вообще не вариант. У LEM на этом датасете SoTA (https://paperswithcode.com/sota/time-series-classification-on-eigenworms).

Также отличные результаты на предсказании частоты сердечных сокращений, предсказании поведения динамической мультимасштабной системы, определении голосовых команд (датасет Google12) и в языковом моделировании на Penn Tree Bank.

Авторы отдельно поисследовали, какие значения получаются в процессе работы у масштабных коэффициентов. Они принимают сильно разные значения (диапазоном в 7 порядков величины) для разных нейронов и меняются в процессе работы. И кроме того есть степенная зависимость частоты встречаемости этих параметров от их амплитуды. Наверное, это всё что-то значит.

Модель выглядит практически как drop-in замена LSTM. Код умещается на одном экране: https://github.com/tk-rusch/LEM/blob/main/psMNIST/network.py

Стоит попробовать в следующий раз, когда будет мысль применить LSTM или что-то подобное.