l
Size: a a a
2018 November 11
С этим уже трудно что-то сделать, гугол топит за js, даже серверы на нём пишут.
Зато есть стимул делать более мощное железо и емкую оперативку. Экономика работает!
Б(
У меня стоковый телеграмХ.
DS
Зато есть стимул делать более мощное железо и емкую оперативку. Экономика работает!
точняк! все пороки человечества в одном месте...
l
А потом на плюсах написать софт и он будет просто летать ^^
DS
У меня стоковый телеграмХ.
и у меня
l
Нейросеточки там. ИИ сам себя на текущем этапе не построит
Б(
А потом на плюсах написать софт и он будет просто летать ^^
Суть в том что на плюсах писать труднее.
l
Я в курсе. Времени больше требуется чем взять пару библиотек и на js за пять минут нашкрябать
DS
Суть в том что на плюсах писать труднее.
А знаешь в чем еще прикол?
Я естественно не помню напамять все алгоритмы Брезенхема, последний раз реализовывал их давно, больше 20 лет назад.
Пришлось искать инфу и собирать.
Так вот, в интернете, на удивление, инфа которая есть, почти вся не рабочая.
Я естественно не помню напамять все алгоритмы Брезенхема, последний раз реализовывал их давно, больше 20 лет назад.
Пришлось искать инфу и собирать.
Так вот, в интернете, на удивление, инфа которая есть, почти вся не рабочая.
DS
наткнулся тут на утверждение:
Построение эллипса путем сжатия окружности:
Построение эллипса путем сжатия окружности:
Начнем из точки (a, 0) на окружности и из точки (0, 0) на отрезке. Будем строить эллипс точно так же, как окружность, но смещать текущую точку по y только в том случае, когда такое смещение происходит в текущем шаге уже для отрезка, т.е. построение отрезка как раз и является реализацией сжатия в a/b раз (точнее, его дискретной аппроксимацией).DS
эти слова написаны профессором
DS
DS
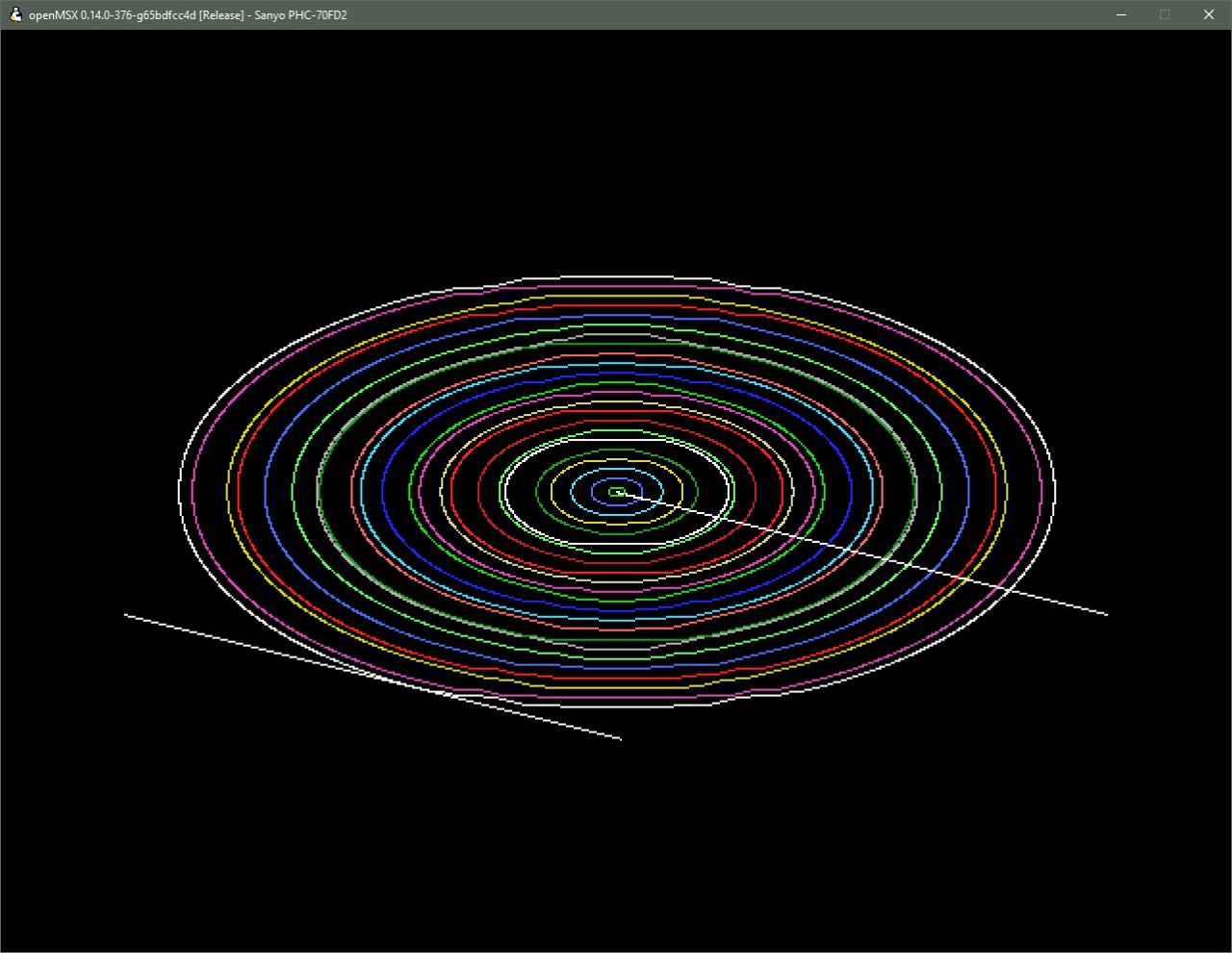
А вот так выглядит сжатие этим методом, причем для Ву, Брезенхема и DDA
DS
можешь сказать что я где-то ошибся, что-то напутал... Но уверяю, я все сделал правильно, тщательно и щепетильно )
DS
переписано с ноля раз шесть
DS
всегда один и тот же эффект
Б(
наткнулся тут на утверждение:
Построение эллипса путем сжатия окружности:
Построение эллипса путем сжатия окружности:
Начнем из точки (a, 0) на окружности и из точки (0, 0) на отрезке. Будем строить эллипс точно так же, как окружность, но смещать текущую точку по y только в том случае, когда такое смещение происходит в текущем шаге уже для отрезка, т.е. построение отрезка как раз и является реализацией сжатия в a/b раз (точнее, его дискретной аппроксимацией).Без контекста выглядит бредом сумасшедшего.
DS
не совсем... теоретически все правильно, и должно работать
DS
Но так как математика целиком целочисленная - не работает.
DS
Если бы работало, был бы супер быстрый алгоритм