Size: a a a
2020 September 25

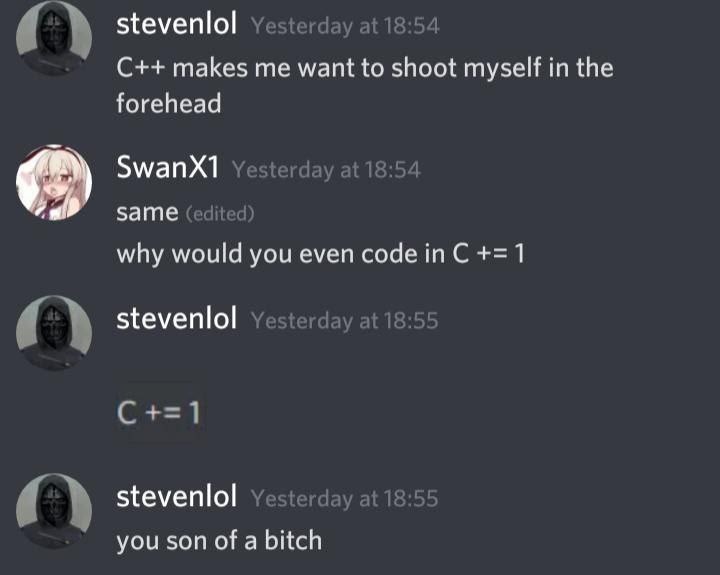
#prog #meme #cpp
2020 September 26

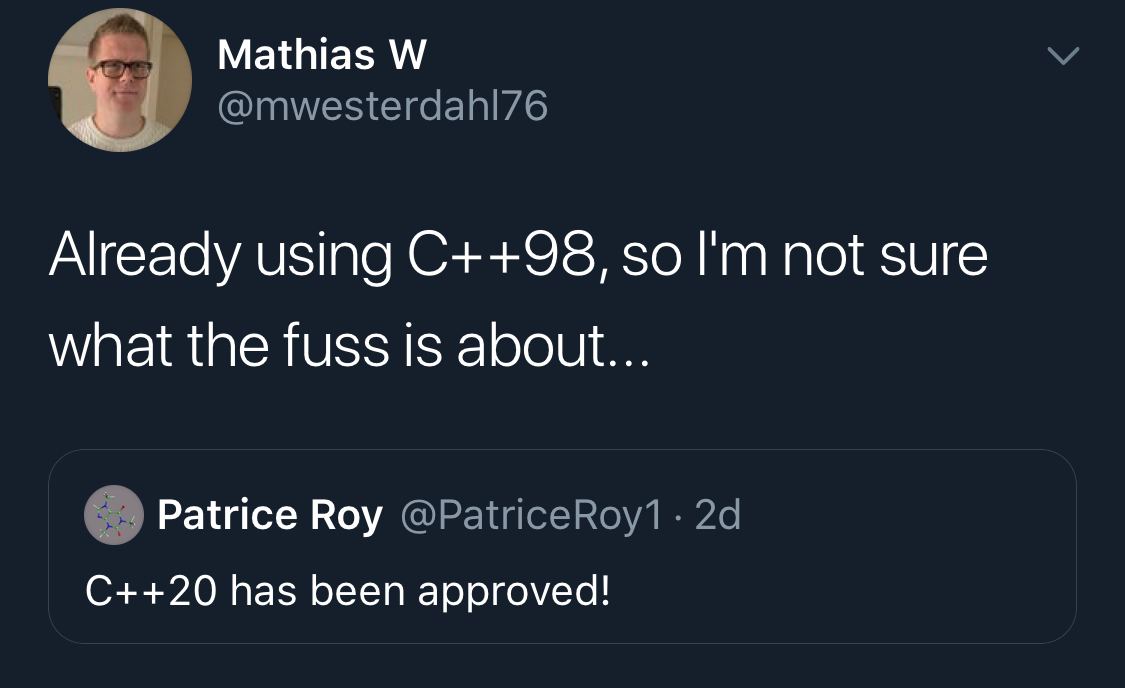
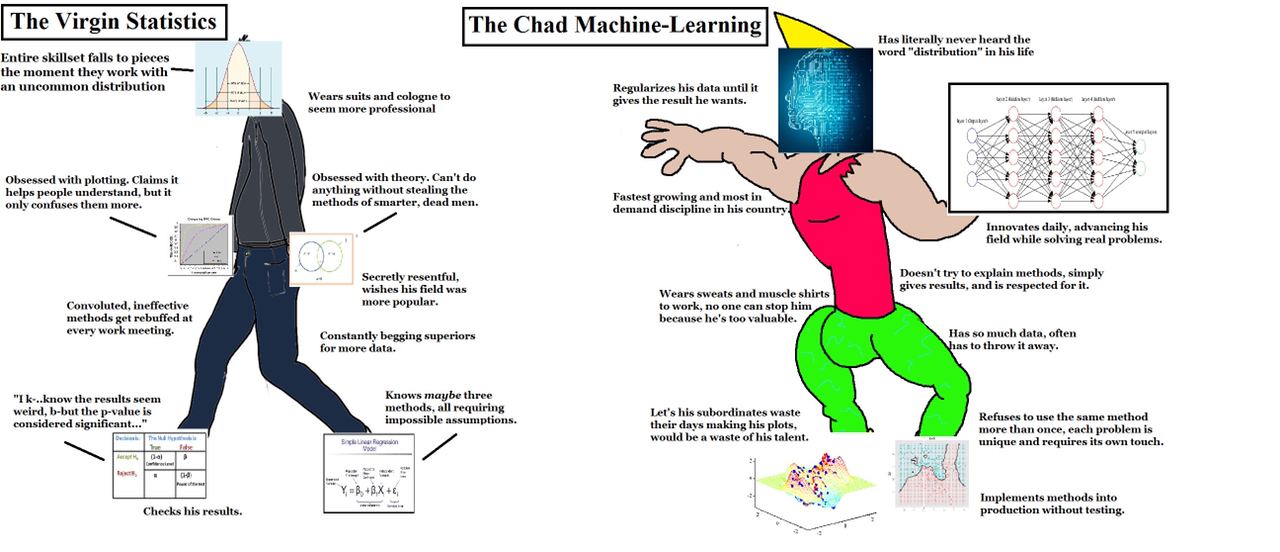
#prog #meme #cpp

Старая поговорка гласит: гуманитарий всегда расстроен, сердит, раздражен и раскаивается.
2020 September 27


#blogrecommendation
Этот канал не существует в вакууме. Есть и другие каналы, которые интересны мне и которые я бы мог назвать друзьями Блог*а. Так что без лишних слов представляю вам их, с описаниями от авторов.
@ihatereality
Личный блог вафли, где он в основном пишет о извращениях с растом. Или просто о чём ему в голову взбредёт. Но в основном о расте.
(^берегите его, он умный и он няша)
@optozorax_dev
Илья программирует всякое и периодически пишет о результатах. При этом он старается объяснить как проблему, так и решение, не забывая ссылаться на известные результаты. Поэтому читатель может узнать что-то новое для себя. Не репостит другие каналы, поэтому контента мало, зато он уникальный.
(а ещё он обожает кастомные клавиатуры)
@ShadyBytes
Личный блог айтишника-либертарианца про технологии и общество. Меньше пресс-релизов крупных компаний, больше личного опыта.
@nlinker_rust
Собираю ржавые и лямбдообразные новости, прикольные цитатки с форумов, ссылки на статьи и всё такое. В-общем, сюда я тащу такие крупицы, которые мне будет жаль потерять в цифровой бездне. Возможно, они покажутся интересными и вам.
@repushko_channel
Один шизоид ругается на IT индустрию и постит иногда смешные мемы.
(любитель философии)
@tipaproit
Типа про IT и вот это вот всё. Прокрастинируем и программируем программы на компьютере. Авторский блог exclusively for Telegram.
@rustamann
(микро) блог @mersinvald о Rust, разработке, и жизни экспата в Германии. Ахтунг! Повышенное содержание мемов.
Этот канал не существует в вакууме. Есть и другие каналы, которые интересны мне и которые я бы мог назвать друзьями Блог*а. Так что без лишних слов представляю вам их, с описаниями от авторов.
@ihatereality
Личный блог вафли, где он в основном пишет о извращениях с растом. Или просто о чём ему в голову взбредёт. Но в основном о расте.
(^берегите его, он умный и он няша)
@optozorax_dev
Илья программирует всякое и периодически пишет о результатах. При этом он старается объяснить как проблему, так и решение, не забывая ссылаться на известные результаты. Поэтому читатель может узнать что-то новое для себя. Не репостит другие каналы, поэтому контента мало, зато он уникальный.
(а ещё он обожает кастомные клавиатуры)
@ShadyBytes
Личный блог айтишника-либертарианца про технологии и общество. Меньше пресс-релизов крупных компаний, больше личного опыта.
@nlinker_rust
Собираю ржавые и лямбдообразные новости, прикольные цитатки с форумов, ссылки на статьи и всё такое. В-общем, сюда я тащу такие крупицы, которые мне будет жаль потерять в цифровой бездне. Возможно, они покажутся интересными и вам.
@repushko_channel
Один шизоид ругается на IT индустрию и постит иногда смешные мемы.
(любитель философии)
@tipaproit
Типа про IT и вот это вот всё. Прокрастинируем и программируем программы на компьютере. Авторский блог exclusively for Telegram.
@rustamann
(микро) блог @mersinvald о Rust, разработке, и жизни экспата в Германии. Ахтунг! Повышенное содержание мемов.

Хочу ли я, чтобы вы подписались на эти каналы? Ну, скорее да, чем нет. Но есть одна небольшая проблема...

Переслано от ilya sheprut
ПОДПИСАН НА ВАФЕЛЯ, АНТОНА, НИКА ЛИНКЕРА И RUSTA::MANN'А
@
ЕСЛИ НОВОСТЬ ИНТЕРЕСНАЯ, ТО ПРИХОДИТСЯ ЧИТАТЬ ЕЁ ПО ЧЕТЫРЕ РАЗА
@
ЕСЛИ НОВОСТЬ ИНТЕРЕСНАЯ, ТО ПРИХОДИТСЯ ЧИТАТЬ ЕЁ ПО ЧЕТЫРЕ РАЗА
2020 September 28

dereference_pointer_there
#prog #article
Можно ли подсчитать производную от регулярного выражения? Можно и нужно!
Статья рассказывает о изученной и эффективной, но почему-то мало известной на практике технике построения распознающих конечных автоматов непосредственно из регулярных выражений. К сожалению, в статье рассматривается лишь задача о соответствии регулярного тексту, в ней ничего не говорится о, скажем, захвате соответствующих частей текста.
"In this paper, we have presented RE derivatives, which are an old, but largely forgotten, technique for constructing DFAs directly from REs. Our experience has been that RE derivatives are a superior technique for generating scanners from REs and they should be in the toolkit of any programmer. Specifically, RE derivatives have the following advantages:
• They provide a direct RE to DFA translation that is well suited to implementation in functional languages.
• They support extended REs almost for free.
• The generated scanners are often optimal in the number of states and are uniformly better than those produced by previous tools.
In addition to presenting the basic RE to DFA algorithm, we have also discussed a number of practical issues related to implementing a scanner generator that is based on RE derivatives, including supporting large character sets"
www.ccs.neu.edu/home/turon/re-deriv.pdf
Можно ли подсчитать производную от регулярного выражения? Можно и нужно!
Статья рассказывает о изученной и эффективной, но почему-то мало известной на практике технике построения распознающих конечных автоматов непосредственно из регулярных выражений. К сожалению, в статье рассматривается лишь задача о соответствии регулярного тексту, в ней ничего не говорится о, скажем, захвате соответствующих частей текста.
"In this paper, we have presented RE derivatives, which are an old, but largely forgotten, technique for constructing DFAs directly from REs. Our experience has been that RE derivatives are a superior technique for generating scanners from REs and they should be in the toolkit of any programmer. Specifically, RE derivatives have the following advantages:
• They provide a direct RE to DFA translation that is well suited to implementation in functional languages.
• They support extended REs almost for free.
• The generated scanners are often optimal in the number of states and are uniformly better than those produced by previous tools.
In addition to presenting the basic RE to DFA algorithm, we have also discussed a number of practical issues related to implementing a scanner generator that is based on RE derivatives, including supporting large character sets"
www.ccs.neu.edu/home/turon/re-deriv.pdf
#prog #article
Почему эта статься называется "Regular-expression derivatives reexamined"? Это не оригинальная статья, а более современный пересказ оригинальной статьи Брзозовски (вот pdf, но читать не советую — это просто довольно грубый скан с бумаги, над нормальной перепечаткой которого никто не заморачивался). Идея производной от регулярного выражения оказалось достаточно плодотворной, чтобы её можно было обобщить до более продвинутых конструкций. Собственно, в этой статье от Мэтта Майта и прочих (pdf) вводится в рассмотрение производная от контекстно-свободных грамматик (CFG), заданных при помощи взаимно-рекурсивных определений, содержащих альтернативы, конкатенацию и звезду Клини, и на основе этого определения реализуется на Racket парсер (именно парсер, а не распознаватель) таких грамматик. Весь код в итоге занял около 30 строк, но для корректной работы полагался на ленивость, мемоизацию и вычисление неподвижных точек функций (есть также реализация на Haskell, но она выглядит так себе, в частности, там зачем-то есть вызов
Как показал себя этот парсер на практике? Паршиво: на разбор 31-строчного синтаксически корректного файла на Python у парсера ушло три минуты. Причина? Неконтролируемые взятия производной от грамматики приводят к тому, что ошмётки грамматики растут экспоненциально. Введение дополнительного шага обработки, названного авторами "сжатием" (compaction) и состоящей в преобразованиях грамматики, уменьшающей её размер, но сохраняющей поведение, привело к желаемому эффекту — повышению производительности. Тем не менее, производительность всё равно осталась достаточно низкой — на разбор того же 31-строчного файла теперь уходило две секунды. Многовато.
Так что же, парсинг с использованием производных (parsing with derivatives, PwD) является непрактичной игрушкой? Отнюдь, как было показано в статье Майкла Адамса. Сложность у этого алгоритма отнюдь не экспоненциальная, как считали авторы, а кубическая. Также оригинальная реализация была написана несколько неоптимально. Во-первых, вычисление неподвижных точек производилось при помощи многократного вызова одной и той же функции, что приводило в худшем случае к квадратичной сложности. Более умная реализация позволяет найти неподвижную точку за линейное время. Во-вторых, в правилах compaction были пропущены парочка правил переписывания грамматики, из-за отсутствия которых грамматика могла прийти в состояние, далёкому от оптимального, но к которому неприменимы операции переписывания. В-третьих, мемоизация в оригинальной реализации использовала хэш-таблицы (причём вложенные). Перемещение мемоизируемых данных из таблиц непосредственно в узлы грамматики положительно сказалось на производительности (надо отметить, что на практике в этих вложенных таблицах было не более одной записи. Хранение единственного значения, разумеется, снизило возможности мемоизации, но, как ни странно, на практике не сильно сказалось на производительности). Итого? Та же идея, но производительность выше на три порядка. Элегантность кода и краткость кода, впрочем, была потеряна.
Можно ли сделать лучше? В принципе, да. Последовательное взятие производной требует многократного прохода по одному и тому же графу, причём, как правило, обход с корня идёт по почти тому же самому пути. Для оптимизации работы над деревьями есть специальная структура данных, zipper (pdf), которая позволяет сфокусироваться на какой-то части дерева и иметь к ней быстрый доступ (кстати, сам автор, Huet, не считает себя изобретателем этой структуры данных, поскольку она переизобреталась неоднократно, статью же он написал главным образом ради того, чтобы идея была более известна). Встраивание зиппера в PwD позволяет повысить его производительность.
⬇️⬇️⬇️
Почему эта статься называется "Regular-expression derivatives reexamined"? Это не оригинальная статья, а более современный пересказ оригинальной статьи Брзозовски (вот pdf, но читать не советую — это просто довольно грубый скан с бумаги, над нормальной перепечаткой которого никто не заморачивался). Идея производной от регулярного выражения оказалось достаточно плодотворной, чтобы её можно было обобщить до более продвинутых конструкций. Собственно, в этой статье от Мэтта Майта и прочих (pdf) вводится в рассмотрение производная от контекстно-свободных грамматик (CFG), заданных при помощи взаимно-рекурсивных определений, содержащих альтернативы, конкатенацию и звезду Клини, и на основе этого определения реализуется на Racket парсер (именно парсер, а не распознаватель) таких грамматик. Весь код в итоге занял около 30 строк, но для корректной работы полагался на ленивость, мемоизацию и вычисление неподвижных точек функций (есть также реализация на Haskell, но она выглядит так себе, в частности, там зачем-то есть вызов
unsafePerformIO).Как показал себя этот парсер на практике? Паршиво: на разбор 31-строчного синтаксически корректного файла на Python у парсера ушло три минуты. Причина? Неконтролируемые взятия производной от грамматики приводят к тому, что ошмётки грамматики растут экспоненциально. Введение дополнительного шага обработки, названного авторами "сжатием" (compaction) и состоящей в преобразованиях грамматики, уменьшающей её размер, но сохраняющей поведение, привело к желаемому эффекту — повышению производительности. Тем не менее, производительность всё равно осталась достаточно низкой — на разбор того же 31-строчного файла теперь уходило две секунды. Многовато.
Так что же, парсинг с использованием производных (parsing with derivatives, PwD) является непрактичной игрушкой? Отнюдь, как было показано в статье Майкла Адамса. Сложность у этого алгоритма отнюдь не экспоненциальная, как считали авторы, а кубическая. Также оригинальная реализация была написана несколько неоптимально. Во-первых, вычисление неподвижных точек производилось при помощи многократного вызова одной и той же функции, что приводило в худшем случае к квадратичной сложности. Более умная реализация позволяет найти неподвижную точку за линейное время. Во-вторых, в правилах compaction были пропущены парочка правил переписывания грамматики, из-за отсутствия которых грамматика могла прийти в состояние, далёкому от оптимального, но к которому неприменимы операции переписывания. В-третьих, мемоизация в оригинальной реализации использовала хэш-таблицы (причём вложенные). Перемещение мемоизируемых данных из таблиц непосредственно в узлы грамматики положительно сказалось на производительности (надо отметить, что на практике в этих вложенных таблицах было не более одной записи. Хранение единственного значения, разумеется, снизило возможности мемоизации, но, как ни странно, на практике не сильно сказалось на производительности). Итого? Та же идея, но производительность выше на три порядка. Элегантность кода и краткость кода, впрочем, была потеряна.
Можно ли сделать лучше? В принципе, да. Последовательное взятие производной требует многократного прохода по одному и тому же графу, причём, как правило, обход с корня идёт по почти тому же самому пути. Для оптимизации работы над деревьями есть специальная структура данных, zipper (pdf), которая позволяет сфокусироваться на какой-то части дерева и иметь к ней быстрый доступ (кстати, сам автор, Huet, не считает себя изобретателем этой структуры данных, поскольку она переизобреталась неоднократно, статью же он написал главным образом ради того, чтобы идея была более известна). Встраивание зиппера в PwD позволяет повысить его производительность.
⬇️⬇️⬇️

dereference_pointer_there
#prog #article
Можно ли подсчитать производную от регулярного выражения? Можно и нужно!
Статья рассказывает о изученной и эффективной, но почему-то мало известной на практике технике построения распознающих конечных автоматов непосредственно из регулярных выражений. К сожалению, в статье рассматривается лишь задача о соответствии регулярного тексту, в ней ничего не говорится о, скажем, захвате соответствующих частей текста.
"In this paper, we have presented RE derivatives, which are an old, but largely forgotten, technique for constructing DFAs directly from REs. Our experience has been that RE derivatives are a superior technique for generating scanners from REs and they should be in the toolkit of any programmer. Specifically, RE derivatives have the following advantages:
• They provide a direct RE to DFA translation that is well suited to implementation in functional languages.
• They support extended REs almost for free.
• The generated scanners are often optimal in the number of states and are uniformly better than those produced by previous tools.
In addition to presenting the basic RE to DFA algorithm, we have also discussed a number of practical issues related to implementing a scanner generator that is based on RE derivatives, including supporting large character sets"
www.ccs.neu.edu/home/turon/re-deriv.pdf
Можно ли подсчитать производную от регулярного выражения? Можно и нужно!
Статья рассказывает о изученной и эффективной, но почему-то мало известной на практике технике построения распознающих конечных автоматов непосредственно из регулярных выражений. К сожалению, в статье рассматривается лишь задача о соответствии регулярного тексту, в ней ничего не говорится о, скажем, захвате соответствующих частей текста.
"In this paper, we have presented RE derivatives, which are an old, but largely forgotten, technique for constructing DFAs directly from REs. Our experience has been that RE derivatives are a superior technique for generating scanners from REs and they should be in the toolkit of any programmer. Specifically, RE derivatives have the following advantages:
• They provide a direct RE to DFA translation that is well suited to implementation in functional languages.
• They support extended REs almost for free.
• The generated scanners are often optimal in the number of states and are uniformly better than those produced by previous tools.
In addition to presenting the basic RE to DFA algorithm, we have also discussed a number of practical issues related to implementing a scanner generator that is based on RE derivatives, including supporting large character sets"
www.ccs.neu.edu/home/turon/re-deriv.pdf
⬆️⬆️⬆️
Первая статья (pdf) (июнь 2020!), с подходом, адаптировавшим зипперы к PwD, использует понятия синтаксиса (как единого объекта) и сфокусированного синтаксиса, который суть синтаксис плюс стек слоёв, который можно к нему применить (отчасти напоминает то, о чём говорил я). Ограничив себя LL(1)-грамматиками, авторы сумели реализовать парсер, работающий за время, пропорциональное количеству входных лексем, причём все важные свойства промежуточных операций они верифицировали при помощи доказательств на Coq. Сам парсер доступен в виде библиотеки на Scala.
Вторая статья (август 2020!) не ограничивается LL(1)-грамматиками, а даёт способ парсить произвольные контекстно-свободные грамматики. Т. к. на вход подаётся лишь единственное правило, алгоритму приходится разбираться с произвольными графами с циклами и использовать несколько изощрённое обобщение зиппера. Статья ценна тем, что в ней реализация выводится через ряд промежуточных версий (одним из шагов, как и в статье Майкла Адамса, является замена таблицы мемоизаций на единственное значение для мемоизации). Получившийся парсер короче оригинального PwD и при этом показывает лучшую производительность, чем оптимизированный PwD Майкла Адамса. К сожалению, не смотря на то, что данный парсер, по всей видимости, имеет кубическую производительность для худшего случая, доказать этот факт авторы не сумели из-за приличного количества нетривиальной логики с мемоизацией.
Как вам уже известно, я выкладываю лишь то, что прочитал/посмотрел сам. Последние две статьи я прочитал, но, к сожалению, не уяснил полностью излагаемые там алгоритмы. Буду перечитывать.
Первая статья (pdf) (июнь 2020!), с подходом, адаптировавшим зипперы к PwD, использует понятия синтаксиса (как единого объекта) и сфокусированного синтаксиса, который суть синтаксис плюс стек слоёв, который можно к нему применить (отчасти напоминает то, о чём говорил я). Ограничив себя LL(1)-грамматиками, авторы сумели реализовать парсер, работающий за время, пропорциональное количеству входных лексем, причём все важные свойства промежуточных операций они верифицировали при помощи доказательств на Coq. Сам парсер доступен в виде библиотеки на Scala.
Вторая статья (август 2020!) не ограничивается LL(1)-грамматиками, а даёт способ парсить произвольные контекстно-свободные грамматики. Т. к. на вход подаётся лишь единственное правило, алгоритму приходится разбираться с произвольными графами с циклами и использовать несколько изощрённое обобщение зиппера. Статья ценна тем, что в ней реализация выводится через ряд промежуточных версий (одним из шагов, как и в статье Майкла Адамса, является замена таблицы мемоизаций на единственное значение для мемоизации). Получившийся парсер короче оригинального PwD и при этом показывает лучшую производительность, чем оптимизированный PwD Майкла Адамса. К сожалению, не смотря на то, что данный парсер, по всей видимости, имеет кубическую производительность для худшего случая, доказать этот факт авторы не сумели из-за приличного количества нетривиальной логики с мемоизацией.
Как вам уже известно, я выкладываю лишь то, что прочитал/посмотрел сам. Последние две статьи я прочитал, но, к сожалению, не уяснил полностью излагаемые там алгоритмы. Буду перечитывать.

А вас когда-нибудь сбивал автомобиль?


#prog #meme
Какой же ор
Какой же ор

#prog #python

Почему в software engineering так сложно с оценками сроков? Потому что зачастую практически невозможно на глазок оценить глубины кроличьей норы, если речь идет о чем-то сложнее перекраски кнопки на лендинге.
Вот небольшой пример. Есть сервис на питоне, в котором некоторые запросы начали тормозить. Хочется найти эти запросы, для этого - добавить в логи какой-то
Но в мире асинхронного питона нельзя просто хранить какой-то id на уровне треде, т.к. тред может переключаться между запросами в процессе await, нужно использовать ContextVars. Чтобы прикрутить ContextVars, нужен Python 3.7+, нужно обновиться. В процессе обновления выясняется, что некоторая старая версия библиотеки официально не поддерживает новый питон, нужно собрать ее руками. Методом проб и ошибок находим коммит, с которого собиралась старая версия для старого питона, собираем для нового питона - результаты не сходятся, тесты падают!
Для начала нужно собрать минимальный воспроизводимый пример (в моем случае получился Dockerfile на 50 строк и примерно столько же Python-кода). Разбираем билд и видим, что библиотеке нужен с десяток shared зависимостей, для которых не всегда указаны версии. Можно найти какие-то древние логи на CI-сервере, который собирал библиотеку для старого питона, и из них достать какие-то куски информации. Их не хватает, и версии приходится перебирать бинарным поиском. Версии подобраны, они конфликтуют друг с другом, и склеить их вместе можно только странным перебором
На все эти развлечения ушло уже три дня, и я не могу сказать, что приблизился к заветным
Вот небольшой пример. Есть сервис на питоне, в котором некоторые запросы начали тормозить. Хочется найти эти запросы, для этого - добавить в логи какой-то
request_id.Но в мире асинхронного питона нельзя просто хранить какой-то id на уровне треде, т.к. тред может переключаться между запросами в процессе await, нужно использовать ContextVars. Чтобы прикрутить ContextVars, нужен Python 3.7+, нужно обновиться. В процессе обновления выясняется, что некоторая старая версия библиотеки официально не поддерживает новый питон, нужно собрать ее руками. Методом проб и ошибок находим коммит, с которого собиралась старая версия для старого питона, собираем для нового питона - результаты не сходятся, тесты падают!
Для начала нужно собрать минимальный воспроизводимый пример (в моем случае получился Dockerfile на 50 строк и примерно столько же Python-кода). Разбираем билд и видим, что библиотеке нужен с десяток shared зависимостей, для которых не всегда указаны версии. Можно найти какие-то древние логи на CI-сервере, который собирал библиотеку для старого питона, и из них достать какие-то куски информации. Их не хватает, и версии приходится перебирать бинарным поиском. Версии подобраны, они конфликтуют друг с другом, и склеить их вместе можно только странным перебором
apt install ... && apt remove ... && apt install. На все эти развлечения ушло уже три дня, и я не могу сказать, что приблизился к заветным
request_id. А ведь сторонний наблюдатель с навыками эффективного менеджера вполне мог бы возмутиться: "че там делать вообще? завел переменную и клади в лог, делов-то".
Иронично, что даже в этом примере кроличья нора в итоге оказалась ощутимо глубже, чем я думал.
Сервис, над которым я работаю, не просто асинхронный, но местами еще и многопоточный: тяжелые операции живут в отдельных тредах. Их как раз и хочется трейсить больше всего. Соответственно, вдобавок нужно прокидывать
Здесь могла быть классическая картинка про многопоточность.
Сервис, над которым я работаю, не просто асинхронный, но местами еще и многопоточный: тяжелые операции живут в отдельных тредах. Их как раз и хочется трейсить больше всего. Соответственно, вдобавок нужно прокидывать
request_id внутрь этих тредов, обновлять там логгеры, и, конечно, нужно реализовать все это в общем виде (больше замыканий богу замыканий!). Здесь могла быть классическая картинка про многопоточность.

dereference_pointer_there
#prog #rust #amazingopensource
Хозяйке на заметку
Подборка библиотек для работы с serde от замечательного Толяна dtolnay.
erased-serde — трейты из serde со стёртыми типами. Позволяют сделать из (де)сериализаторов трейт-объекты. Обычно это запрещено правилами object safety из-за наличия обобщённых типов.
typetag — сериализация и десериализация трейт-объектов. Работает на костылях.
serde-repr — делегирует (де)сериализацию C-like enum его числовому значению.
serde-stacker — позволяет десериализовывать глубоко вложенные структуры, динамически выделяя память под стек. Работает, увы, не на всех OS: нормально работает на linux и MacOS и течёт на Windows.
serde-ignored — позволяет обернуть десериализатор с кастомный коллбеком, который будет вызываться на всех проигнорированных в процессе десериализации ключах.
Хозяйке на заметку
Подборка библиотек для работы с serde от замечательного Толяна dtolnay.
erased-serde — трейты из serde со стёртыми типами. Позволяют сделать из (де)сериализаторов трейт-объекты. Обычно это запрещено правилами object safety из-за наличия обобщённых типов.
typetag — сериализация и десериализация трейт-объектов. Работает на костылях.
serde-repr — делегирует (де)сериализацию C-like enum его числовому значению.
serde-stacker — позволяет десериализовывать глубоко вложенные структуры, динамически выделяя память под стек. Работает, увы, не на всех OS: нормально работает на linux и MacOS и течёт на Windows.
serde-ignored — позволяет обернуть десериализатор с кастомный коллбеком, который будет вызываться на всех проигнорированных в процессе десериализации ключах.
#prog #rust
serde-diff
"A small helper that can
1. Serialize the fields that differ between two values of the same type
2. Apply previously serialized field differences to other values of the same type."
serde-diff
"A small helper that can
1. Serialize the fields that differ between two values of the same type
2. Apply previously serialized field differences to other values of the same type."