мне кажется, это абсолютный неадекват

сейчас темно после работы только тупо зимой, с весны по конец осени вполне себе светло
а вот по утру есть вариации

не вполне себе светло. я в москве  жил, на себе проверил,что такое когда в 19 вышел с работы в апреле, а уже темнеет.

да блядь не москва тут

ты говоришь что в других городах пофиг, так вот нет

а у вас должно быть ещё раньше весной садится солнце (в равноденствие и в апреле длина дня примерно одинакова)

у нас солнце ОООЧЕНЬ быстро встаёт и садится

подздравляю

грубо говоря в 6-30 ещё темень, а в 7-30 уже всё прекрасно видно

поэтому не надо южный город равнять с москвой, это всё равно что по краснодару отопление в Воркуте делать

​​ЛЮБОВЬ К ЦИФРЕ 9

Этот пост будет посвящен не словам, а цифрам. Ну а что? Их холодный жар, как сказал поэт, нам тоже внятен. К тому же то, о чем мы собираемся говорить, имеет скорее семиотическое измерение.

Есть такой закон Бенфорда. Он говорит, что если вы возьмете некое множество чисел, описывающих количественную сторону той или иной сферы реальной жизни и способных расти экспоненциально, то распределение первых цифр в этих числах будет выглядеть так:

1 — 0.301,
2 — 0.176,
3 — 0.125,
4 — 0.097,
5 — 0.079,
6 — 0.067,
7 — 0.058,
8 — 0.051,
9 — 0.046.

Иными словами, чем меньше цифра, тем выше вероятность встретить ее в начале числа. Понятно, что, как и всякий эмпирический закон, закон Бенфорда не строг и точные доли реальных цифр могут существенно отличаться от прогнозируемых, однако тот факт, что начальная единица и начальная девятка встречаются чаще и реже всех остальных соответственно, был продемонстрирован на множестве разнородных примеров — от высоты самых высоких зданий в мире до количества жителей американских городов.

Проверка распределения первых цифр по закону Бенфорда широко используется для выявления манипуляций с данными. Если числа не отражают реальной картины действительности, а просто выдуманы кем-то из головы, скорее всего, частотность их первых цифр будет резко отличаться от приведенного выше инварианта.

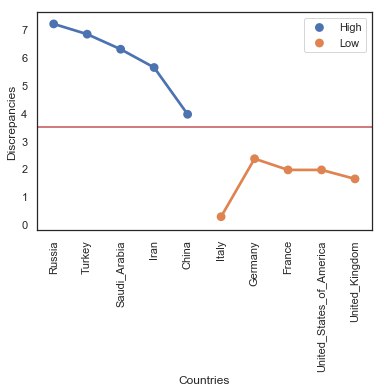
Для нашего опыта мы использовали данные о ежедневной смертности от коронавируса в разных странах за весь период наблюдений, доступные здесь: https://data.europa.eu/euodp/en/data/dataset/covid-19-coronavirus-data. Нас интересовала в первую очередь цифра 9. Мы высчитали, насколько ее частота появления в качестве первой цифры чисел официальной статистики отличается от прогнозируемой по закону Бенфорда.

Результаты представлены на графике. Первые пять позиций по оси икс (синий цвет) — страны с максимальным расхождением во всей базе данных. Другие пять позиций (оранжевый цвет) — сравнительные показатели главных европейских стран и США.

Сделать из всего этого выводы мы предоставим — в качестве интеллектуального упражнения — читателю.

Задать вопрос @UchenyjBot

⚡️ Марка Datsun уходит из России. Будете скучать? https://motor.ru/news/datsun-russia-28-05-2020.htm?utm_source=motortg&utm_medium=social

просто не надо всех в один часовой пояс запихивать, а потом стараться то одним, то другим угодить

вместо московского пояса должно быть 3 — Питер, Москва и Казань

видел уже эту новость, закрыл тут же как открыл — пофиг

А Нижний к кому?

то же

я бы ещё потерпел, наверное

по Оке поделить

спорная статья

Кек