A
Size: a a a
2020 December 10
Anna Kimerene
надо голосовать за КПРФ, чтобы выдавить ЕДРО из Госдумы...К едра большинство в ГосДуме, именно поэтому принимаются все антинародные законы!
Когда там следующие выборы?
К
Olesya
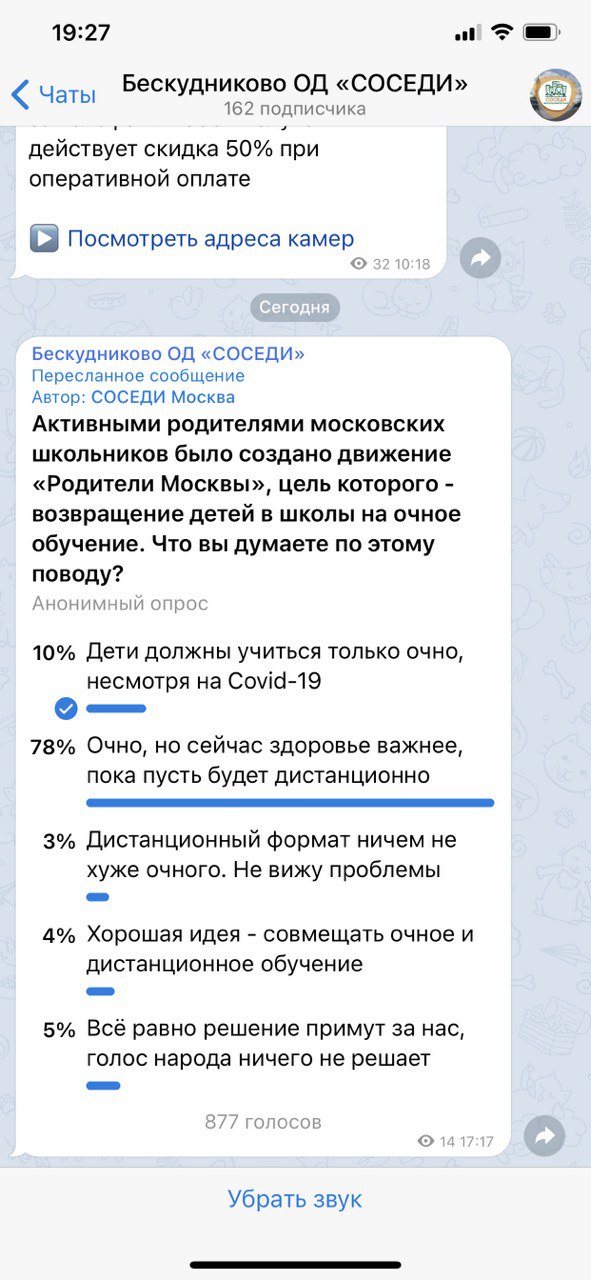
Что это?откуда голоса,?
Y
📍ЧАТЫ ПО ОКРУГАМ:
САО ВАО ЮВАО
ЗАО ЮАО ЦАО
СЗАО ЮЗАО СВАО
МО ЗелАО ТинАО
🇷🇺РОДИТЕЛИ РЕГИОНОВ
Воронеж
Краснодар
Красноярск
Новосибирск
Санкт-Петербург
Саратов
Сочи
Ханты-Мансийск
‼️Внимание‼️ Общественное Движение Родители Москвы не несет ответственность за группы, созданные родителями.
✴️✴️✴️✴️✴️✴️✴️✴️✴️✴️✴️✴️✴️
САО ВАО ЮВАО
ЗАО ЮАО ЦАО
СЗАО ЮЗАО СВАО
МО ЗелАО ТинАО
🇷🇺РОДИТЕЛИ РЕГИОНОВ
Воронеж
Краснодар
Красноярск
Новосибирск
Санкт-Петербург
Саратов
Сочи
Ханты-Мансийск
‼️Внимание‼️ Общественное Движение Родители Москвы не несет ответственность за группы, созданные родителями.
✴️✴️✴️✴️✴️✴️✴️✴️✴️✴️✴️✴️✴️
И
Angel
Честно. Не голосовала за них. О чем сейчас жалею. Теперь буду!
А все равно победит кто? Правильно ... медведь
A
Ирина
А все равно победит кто? Правильно ... медведь
Ну почему же. Не факт
ИЛ
Я под большим впечатлением от Круглого стола! Молодцы какие все! Кроме Жирика! Какой мальчик старшеклассник: как говорит! Поддерживаю
A
Olesya

Да пусть сидят сколько влезет. Мы сидеть не будем
A
Иванова Людммла
Я под большим впечатлением от Круглого стола! Молодцы какие все! Кроме Жирика! Какой мальчик старшеклассник: как говорит! Поддерживаю
Я тоже)) очень хорошее заседание было. Главное с людьми, с народом! А не в закрытых стенах, как обычно
М
Иванова Людммла
Я под большим впечатлением от Круглого стола! Молодцы какие все! Кроме Жирика! Какой мальчик старшеклассник: как говорит! Поддерживаю
Мальчик - образцовый. Спасибо родителям. Низкий поклон за воспитание. Патриот Родины. Почти забытое слово.
НП
Наталья
Вы не поверите, последнее время ставила галочку на против этой партии...
Чтоб хоть как то разбавить единоросов...
Ну ни как не получается, все знают как прогодит подсчет голосов
Чтоб хоть как то разбавить единоросов...
Ну ни как не получается, все знают как прогодит подсчет голосов
А у нас получилось!С небольшим перевесом,но прошёл таки
✊✊
Angel
Я тоже)) очень хорошее заседание было. Главное с людьми, с народом! А не в закрытых стенах, как обычно
И... без масок✊✊✊не так страшен чорт, как нам его малюют!!
A
✊ ✊
И... без масок✊✊✊не так страшен чорт, как нам его малюют!!
Вот тоже понравилось) сильные люди, смелые!
ТФ
👩🏫Разберём "становление математики", каким его видят авторы с канала ВЕКТОР.
https://youtu.be/GIdBRn6wMp8
📔Видео начинается с цитаты Энгельса из Анти-Дюринга, всем известного философского до зубовного скрежета трактата, где сам Энгельс вольно рассуждает о математике, дескать согрешила. Утратила состояние абсолютной значимости, когда приняла переменные величины.
🙋🏻♀️А кстати, когда?
Когда люди перестали понимать, что же они делают, интегрируя? Начали веровать в некое абстрактное "потому что раньше получалось верно"?
Наверное, в древнем Китае, где решали уравнения высших степеней? Действительно, с тех пор у общества явные проблемы с пониманием происходящего (выражающиеся в росте производительных сил?)
🗣️Первое самостоятельное утверждение автора: утверждение о том, что необходимо двигать вперёд математику (да!) А для этого надо понимать логику её развития (действительно, неплохо бы!)
Для того, чтоб разъяснить логику развития науки, автор начинает с отвлеченных суждений о категориях. Мы узнаем о больше/меньше/равно, и в тот момент когда я уже приготовилась услышать о столь любимой Марксом в первом томе пропорции, съезжает с темы, говоря о "более сложных". Очень жаль, ведь именно чтобы узнать об этих более сложных, мы и включили это видео.👀
Говоря о системах счисления (зачем? Ведь мы не показываем связи ни с остальной математикой, на напрямую с уровнем производительных сил) автор говорит о переходе к десятичной системе счисления, утверждая что это стало возможным благодаря появлению нуля.
✒️Здесь хочу оставиться подробнее.
Видимо имелся в виду переход от непозиционнных систем счисления к позиционным.
Но где же тогда так любимое философами и действительно уместное здесь рассуждение о количественных и порядковых числах?
И почему, говоря о системах счисления, мы зачем-то вспоминаем про счёт на ногах, но молчим о счёте на фалангах пальцев, оставившем нам в виде рудимента 60 минут в часе?⏲️
👍Очень отрадно слышать, что появление частной собственности, а с ней и государства, дало толчок к развитию математики. Жаль, что больше схожих рифм автор найти не удосужился. Хотя вероятно именно на них следовало бы сделать акцент, говоря о становлении математики как науки и о контексте её исторического развития.
Я приготовилась послушать о необходимости тригонометрии для навигации, архитектуры и астрономии, а также о развитии этой области, но видимо авторы не считают это достаточно весомым, чтоб упоминать в ролике. 🤷🏻♀️
После возникновения нуля в уравнениях у автора закономерно наступает матанализ, сразу в семнадцатом веке. Вот уж не знаю, насколько такое разделение на "древнюю старину" и "современные очертания математики" удобно для заявленной цели ролика, для иллюстрации становления математики как науки. У меня сложилось впечатление, что "оно само, я ничего не трогала!"(с).
И уж действительно странно столько говорить об эпохе интенсивного развития матанализа, не связав это с исторической эпохой, когда сам матанализ был необходим. Не показав, как математическая мысль проецируется на инженерную, и как они вместе творят прогресс.
📝При этом почти три минуты из девяти минут ролика посвящены философствованию о явлении гениальности, о том, что выдающиеся идеи одновременно приходят не в одну гениальную седовласую голову.
При этом ещё почти две минуты (из девяти, да) товарищ рассказывает об актуальных математических проблемах, которые толком не в силах интерпретировать, потому что для этого надо гораздо, значительно больше времени.
✏️Словом, весь ролик, вместе с предложением автора "по поводу ваших вопросов напишите в личку Эмилии Балбус, и обсудите с ней, где же именно ломается математика" производит впечатление "мопед не мой, я только разместил объяву"(с).🛵
👩🏻🏫Что ж, если до нас этого не сделали, попробуем подать блюдо "становление математики" под соусом из диамата самостоятельно.
🎥Пока монтирую ролики сама. Буду рада финансовой помощи, потому что сейчас основная работа отнимает очень много времени.
https://youtu.be/GIdBRn6wMp8
📔Видео начинается с цитаты Энгельса из Анти-Дюринга, всем известного философского до зубовного скрежета трактата, где сам Энгельс вольно рассуждает о математике, дескать согрешила. Утратила состояние абсолютной значимости, когда приняла переменные величины.
🙋🏻♀️А кстати, когда?
Когда люди перестали понимать, что же они делают, интегрируя? Начали веровать в некое абстрактное "потому что раньше получалось верно"?
Наверное, в древнем Китае, где решали уравнения высших степеней? Действительно, с тех пор у общества явные проблемы с пониманием происходящего (выражающиеся в росте производительных сил?)
🗣️Первое самостоятельное утверждение автора: утверждение о том, что необходимо двигать вперёд математику (да!) А для этого надо понимать логику её развития (действительно, неплохо бы!)
Для того, чтоб разъяснить логику развития науки, автор начинает с отвлеченных суждений о категориях. Мы узнаем о больше/меньше/равно, и в тот момент когда я уже приготовилась услышать о столь любимой Марксом в первом томе пропорции, съезжает с темы, говоря о "более сложных". Очень жаль, ведь именно чтобы узнать об этих более сложных, мы и включили это видео.👀
Говоря о системах счисления (зачем? Ведь мы не показываем связи ни с остальной математикой, на напрямую с уровнем производительных сил) автор говорит о переходе к десятичной системе счисления, утверждая что это стало возможным благодаря появлению нуля.
✒️Здесь хочу оставиться подробнее.
Видимо имелся в виду переход от непозиционнных систем счисления к позиционным.
Но где же тогда так любимое философами и действительно уместное здесь рассуждение о количественных и порядковых числах?
И почему, говоря о системах счисления, мы зачем-то вспоминаем про счёт на ногах, но молчим о счёте на фалангах пальцев, оставившем нам в виде рудимента 60 минут в часе?⏲️
👍Очень отрадно слышать, что появление частной собственности, а с ней и государства, дало толчок к развитию математики. Жаль, что больше схожих рифм автор найти не удосужился. Хотя вероятно именно на них следовало бы сделать акцент, говоря о становлении математики как науки и о контексте её исторического развития.
Я приготовилась послушать о необходимости тригонометрии для навигации, архитектуры и астрономии, а также о развитии этой области, но видимо авторы не считают это достаточно весомым, чтоб упоминать в ролике. 🤷🏻♀️
После возникновения нуля в уравнениях у автора закономерно наступает матанализ, сразу в семнадцатом веке. Вот уж не знаю, насколько такое разделение на "древнюю старину" и "современные очертания математики" удобно для заявленной цели ролика, для иллюстрации становления математики как науки. У меня сложилось впечатление, что "оно само, я ничего не трогала!"(с).
И уж действительно странно столько говорить об эпохе интенсивного развития матанализа, не связав это с исторической эпохой, когда сам матанализ был необходим. Не показав, как математическая мысль проецируется на инженерную, и как они вместе творят прогресс.
📝При этом почти три минуты из девяти минут ролика посвящены философствованию о явлении гениальности, о том, что выдающиеся идеи одновременно приходят не в одну гениальную седовласую голову.
При этом ещё почти две минуты (из девяти, да) товарищ рассказывает об актуальных математических проблемах, которые толком не в силах интерпретировать, потому что для этого надо гораздо, значительно больше времени.
✏️Словом, весь ролик, вместе с предложением автора "по поводу ваших вопросов напишите в личку Эмилии Балбус, и обсудите с ней, где же именно ломается математика" производит впечатление "мопед не мой, я только разместил объяву"(с).🛵
👩🏻🏫Что ж, если до нас этого не сделали, попробуем подать блюдо "становление математики" под соусом из диамата самостоятельно.
🎥Пока монтирую ролики сама. Буду рада финансовой помощи, потому что сейчас основная работа отнимает очень много времени.
ЮН
Добрый вечер. Наткнулась сегодня на статью
НП
Angel
Когда там следующие выборы?
В сентябре
И
Наталия Перова
А у нас получилось!С небольшим перевесом,но прошёл таки
А у нас на муниципальном уровне депутат - директор нашей школы, едрос. Вот и требуй от них после этого








