Какая именно сумма?

То есть из двух клеток, сверху и сбоку, какую выбрать?

Или ты предлагаешь сумму хранить в отдельной размерности? Так максимальная сумма же n*m будет

Представь что состояния -- это вершины графа

А переходы -- рёбра

Теперь нужно просто посчитать количество путей

Да

А почему n*m*(n+m)? Таблица n*m, ещё и сумма максимум n*m

А, ой

Я дурак, понял)

Сумма максимум линейная

n+m-1, да, я наверное не выспался)

Получается задачу можно решить за n*m*(n+m)/64 с битсетами, круто!

Спасибо

Не за что)
А как там битсеты юзать?

Третья размерность это наша сумма - она либо есть, либо нет.
Создаём массив битсетов b[n][m] размера n+m.
Бит в битсете говорит нам, можно ли найти путь который заканчивается в данной точке или нет с такой суммой. Тогда при переходе мы можем скопировать битсет и сдвинуть его в нужную сторону. (Аккуратно обработав случаи с минимальной суммой, например создать битсет размера 2(n+m) и положить начало координат в центре)

А понял

Я думал там количество маршрутов нужно

is there an english group

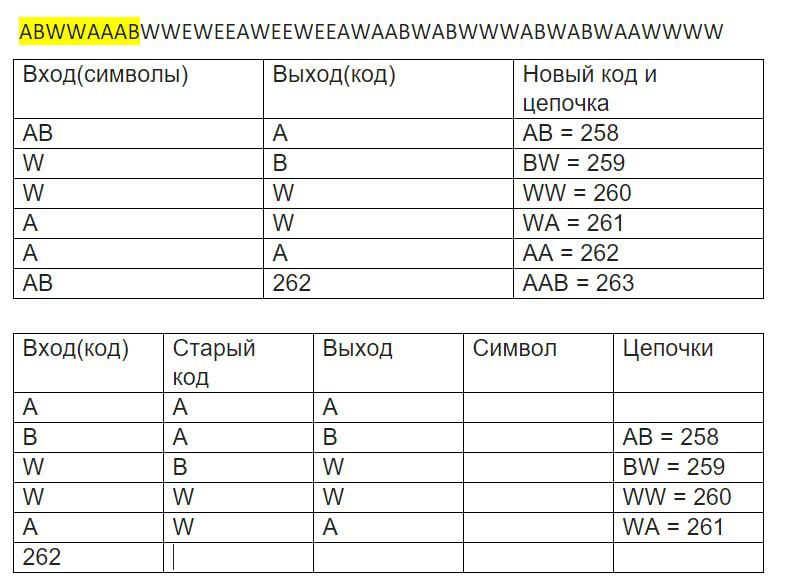
Подскажите что делать в этой ситуации ?

Я дохожу до этого места и у мне нужно взять код 262 из таблица, а этого кода в ней нет
Алгоритм LZW