Он же читает

И сказал

Что программа примерно одна и та же

Типо нам бессмысленно ходить, потому что пересечение почти 100 :

100%

и тут еще есть кое-какие материалы

Годнота-то какая годнота!

Я так и не понял что за фигня с оцениванием происходящего и что стоит делать дома если стоит (кроме теханья одной задачки).

Годнота — это это http://wiki.cs.hse.ru/Дискретная_математика_1_2016/2017
Оно хотя бы структурировано.
И по темам более полезно для многих.

Я тоже не очень понял
Но он говорил что-то вроде "в присылаемой домашке проверяться тоже будут не все задачи, а самые интересные" или что-то такое, так что, как я понял, домашку нужно решать и присылать всё-таки

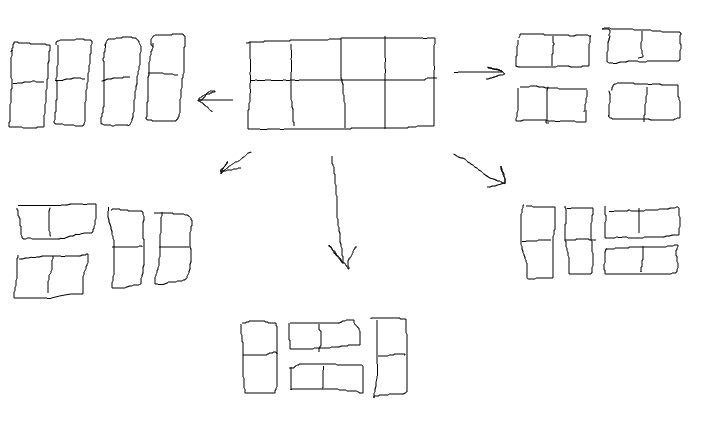
Вот представим плитку шоколадки 2x4. Её можно поделить на плитки размером 2x1 аж 5 способами:

Рисовал мышкой, поэтому неровно)

Сколькими способами делится плитка размером 2 x n?

Если кто хочет подумать сам, не читайте дальше, а пролистайте чатик, чтобы ответ оказался внизу (или сверните), и думайте.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

Обозначим число способов для плитки 2 x n как F(n).
Посмотрим на самый нижний самый левый квадратик.
Он принадлежит либо вертикальной плитке, и тогда всё остальное можно поделить F(n - 1) способами.
Либо же он принадлежит горизонтальной плитке, тогда автоматически квадратик над ним принадлежит тоже горизонтальной, а остальную плитку можно поделить F(n - 2) способами.
Таким образом,
F(n) = F(n - 1) + F(n - 2)

Ну ещё заметим для полноты картины, что плитки 2x1 и 2x2 делятся 1 и 2 способами. То есть,
F(1) = 1
F(2) = 2

Ну, собственно, Фибоначчи на этом моменте все узнали, не правда ли?

Небольшой спойлер. У нас будут производящие функции, а значит, скорее всего, мы чуть позже докажем нерекуррентную формулу для чисел Фибоначчи, ту, что через корень из 5.

Её в конце занятия даже на доске написали.

Так её же через линал проще вроде

нет?

Ага, поэтому я и написал "докажем", а не, например, "узнаем".

сколько у нее вообще доказательств