Я после лекции расскажу, если напомните. Но вообще можете посмотреть доклад брендана с последнего котлинконфа

не только

Спасибочки

Так вот. Суть в том, что в математических задача часто нужно знать не только саму функцию, но и ее производную. Например это важно для задач оптимизации, которые важны для анализа данных и машинного обучения. Проблема в том, что обычная числовая функция свою производную не знает и ее надо считать численно или передавать руками при создании функции. Второе - лень (тем более, что может понадобиться вторая производная), а первое приводит к существенному увеличению времени счета и к погрешностям численного дифференцирования. При этом, для любых не слишком заумных функций производную можно  посчитать аналитически на основе ее символьного представления. Теперь встает вопрос, как внутри программы получить это символьное представление, чтобы его продифференцировать. Есть несколько путей. Можно на языковом уровне накрутить алгебраические контексты, в которых математические операции преобразуются в дифференцируемые операции:
https://github.com/mipt-npm/kmath/blob/abe68a4fb6239701ebd0f581b6fafb9047de91e7/kmath-core/src/commonTest/kotlin/kscience/kmath/expressions/SimpleAutoDiffTest.kt#L38
а вот тут даже пример, к которому сразу оптимизация приделана: https://github.com/mipt-npm/kmath/blob/abe68a4fb6239701ebd0f581b6fafb9047de91e7/kmath-commons/src/test/kotlin/kscience/kmath/commons/optimization/OptimizeTest.kt#L58-L61.

Есть могучая либа для автодифа, к которой @commandertvis пилит коннектор: https://github.com/breandan/kotlingrad. Почитайте, там просто офигенная дока.

Второй подход - это заставить компилятор сам разбирать выражение и считать производные. По этому пути пошел сначала свфит, а сейчас фейсбук. Вообще говоря, хороший путь и оба подхода можно совместить. Но конкретно к тому, что сейчас показал фейсбук у меня есть несколько вопросов. В частности, я не понимаю, как в этих раскрашенных скоупах будут добавляться новые операции дифференцирования. В kmath эти операции явно прописаны в вызывающем скоупе.

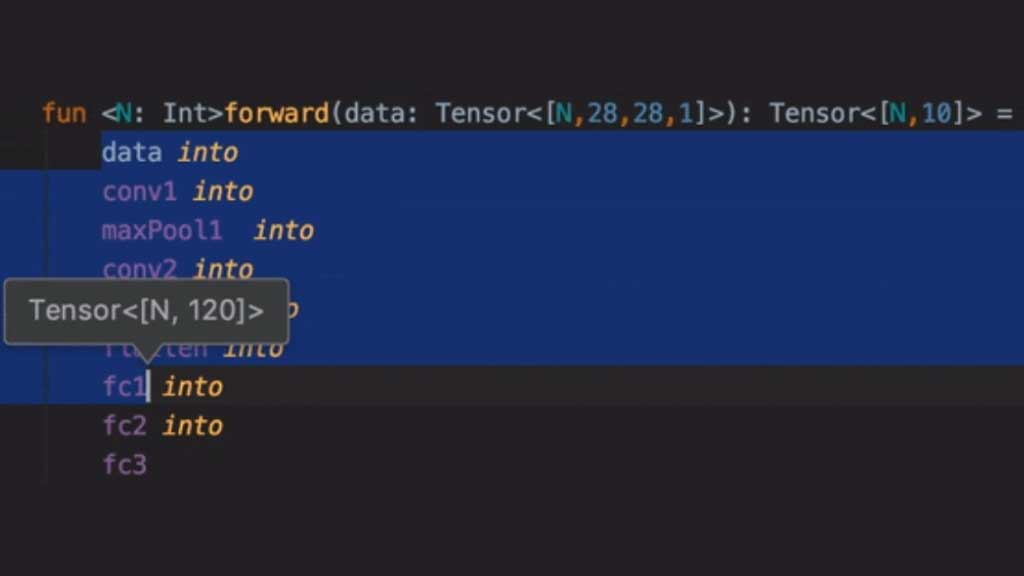
Типирование тензоров по размеру - это другая задача. Смысл в том, чтобы матрицу 3х4 нельзя было умножить на матрицу 2х2. На это опять же есть решения и у Брендана (кодогенерация размерностей аля Асмодей) и у меня (минорная рефлексия с синглетонами).

немного оффтоп вопрос, как вы вставляете куски кода, что у них другой шрифт?

о чем это вы?

например вот сообщение с кодом и просто текстом:

а

выделяете текст и жмёте правой кнопкой мышей

и там форматирование

ааа все, спасибо большое!

Всем привет,

Появилась проблема с запуском приложения на Kotlin(бекенд на ktor, но не суть). Выдает мне ошибку на скрине. Хотя, если собирать приложение, то все работает.

Кто сталкивался, и как чинить? build.gradle.kts сейчас кину

Это не полный лог. Нужно выбрать корневой елемент слева

И вот build.gradle.kts
https://pastebin.com/5D08imZz

А запуск со --stacktrace что говорит?