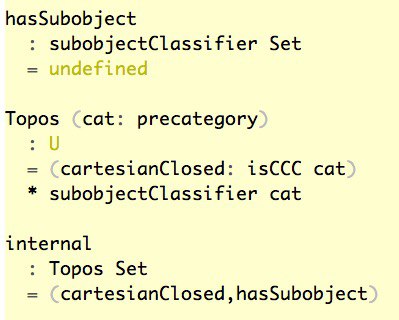
Cartesian Closure of Category of Sets

Кто быстрее меня напишет hasSubobject ? :-)

Оставил для вас самое интересное!

Много новостей произошли за это время напишу только главные. Во-первых создал страницу для topos.ctt, и не в папке /mltt/types, а как статью, прямо в корне /mltt/. Во-вторых написал первый #1 модуль своего курса /tex/articles/mltt/, но там ничего интересного, обычные Пи, Сигма и =, и встраивание MLTT в тайпчекер как пример:
https://github.com/groupoid/groupoid.space/blob/master/tex/articles/mltt/mltt.pdf

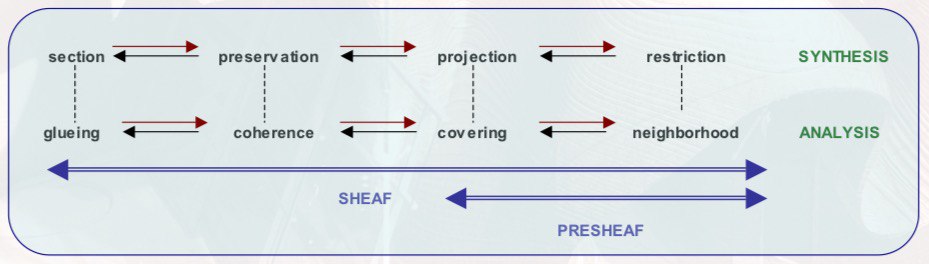
Как ни странно, локальная гомотопическая теория (Jardine) — это хороший пример неизведанного в конструктивном анализе. Чтобы продолжить К-теоретическое направление базовой библиотеки, я посмотрел у Жардина как можно было бы начать это напарвление, и первое с чего нужно начать, это построение геометрической Гротендиковской теории топосов. Я привел три варианта построения топологии для сайта Гротендика (sieves, coverage, covering families). А также построил категорию множеств и показал, что она — это элементарный топос (в определении Ловера-Тьерне). По объему материала на лекцию, которая и запланирована в курсе по номером девять #9 (— к чему такая спешка? — чтобы не отставать от перинатальной топологии!).

Можно пойти дальше и попробовать построить категорию этальных схем (или этальных морфизмов, которые мы уже построили в etale.ctt). Категория пучков на этальном сайте (сюда еще этальная топология как инстанс покрытия подключается) категории этальных морфизмов — это этальный топос схем. Нет, ничего, что нас остановило бы закодировать этальный топос схем на кубике прямо завтра (кроме лени). Этальный топос, на этальном сайте категории этальных морфизмов — главная мотивация Гротендика и локальной алгебраической топологии. Накрывающие семейства тут сурьективные семейства этальных схем. Этальные морфизмы в алг. топологии — это аналог морфизмов сложных аналитических пространств, которые аналитически локально являются изоморфизмами. Когда схема Х есть спектором поля к с абсолютной группой Галуа G, этальный топос схемы Х есть вариантом BG, категории дискретных множеств с непрерывным действием группы G. Когомология в этом случае — это когомология Галуа к. Когомология этальных топосов со значениями в Z/n, где n — простое, являющееся характеристикой к. Благодаря этому можно говорить о Когомологии Вейля и о доказательстве коньюнктуры Вейля. И позже уже об инстансах этих гомологий, когомологиях де Рама, как об современном основании математического анализа с точки зрения теории топосов.

Ссылка на топос категории множеств: http://groupoid.space/mltt/topos/ — там интересно, я старался :-)
Все пул реквесты с typo сюда: https://github.com/groupoid/groupoid.space/blob/master/mltt/topos/index.pug

Kudos to @road21 for Meaningful TeX Fix!

Now officially, https://instagram.com/groupoid.space

Синтаксис кубика на одной картинке

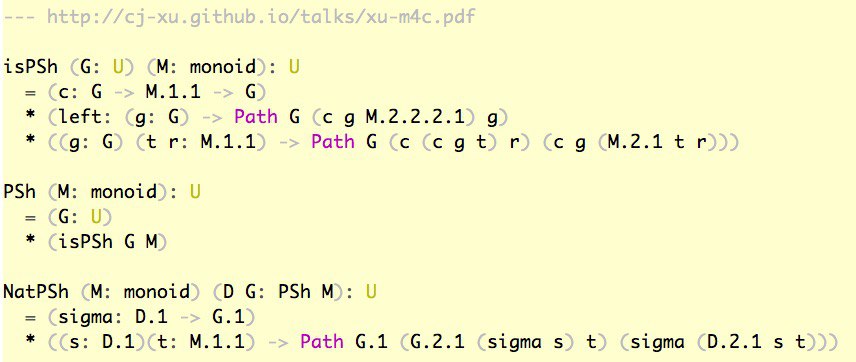
Homotopy Presheaf on Monoid structure

Хотел написать о своей идее. В процессе PhD требуют писать статьи и каждый PhD неплохо было бы если бы подготовил свой курс как он видит предмет. Я наконец-то увидел весь предмет (спустя 3 года) и думаю что для моего математического творчества наиболее подходит следующая упаковка. Чтобы 10 раз не писать одно и то же, я решил объединить диссертацию, курс по HoTT, статьи, и книгу в одну повествовательную линию в виде серии статей или выпусков одного журнала.

Журнал имеет фиксированное количество выпусков разделенных как и курс HoTT на две большие части или тома: Основания и Математика. В первом томе Основании читаются Завтипы или Теория Типов Мартина-Лёфа, Индуктивные типы, Гомотопическая система типов, Высшие индуктивные типы, изоморфизмы, артикль The,  Charles Rezk, Jacob Lurie, Vladimir Voevodsky как открыватели унивалентности. Т.е. только саму основу языка без примеров из математики.

Вторая часть является учебником по математике, который опирается на гомотопическую теорию типов с высшими индуктивными типами как основания (предыдущий том). Тут хочется сделать уклон из HoTT в сторону алгебраической топологии и больше внимания уделить теории топосов и предпучковым моделям теории типов с точки зрения категориальной интерпретации.

Полный список выпусков я вижу следующим образом и значительная часть их уже оформлена, а пустующие заглушки постепенно пополняются картинами из головы. Воспринимайте эту серию как комикс от Групоид Инфинити. https://github.com/groupoid/groupoid.space/tree/master/tex/articles

ОСНОВАНИЯ

Issue I: Intenalizing Martin-L ̈of Type Theory. DONE
Issue II: Inductive Types and Encodings.
Issue III: Homotopy Type Theory.
Issue IV: Higher Inductive Types.
Issue V: Many Faces of Equality.  DONE
Issue VI: Modalities.

МАТЕМАТИКА

Issue VII: Set Theory.
Issue VIII: Category Theory.
Issue IX: Topos Theory. DONE
Issue X: Differential Geometry.
Issue XI: Hopf Fibrations.
Issue XII: Abstract Algebra.
Issue XIII: K-Theory.

ПРИЛОЖЕНИЯ

Addon I: PTS for Erlang (Om) DONE

DONE — есть и статья в скопусе и код и документация на сайте
пустота — есть только термы в базовой библиотеке

Это то что есть прямо сейчас. В недостаточной степени пока проработат материал по теории гомологий и спектральной теории, также есть зачатки теории клеточных простраств как примеру прямого втсраивания CW-комплексов в язык в виде HIT. Тринадцать глав, в целом должно быть веселее чем менее математичный учебник по HoTT, все самое интересное в диссертациях. В дальнейшем попытаюсь написать аннотации человеческим языком по тем работам, которые уже написаны, это около 4-х выпусков, по одному из которых пока есть только домашние задания, и некоторые уже начали их выполнять, что меня очень радует и воодушевляет.

А какие разделы математики интересны вам?

Что хотелось бы видеть в качестве возможного продолжения альманаха:

1. Теория графов как вырожденный случай одномерных CW-комплексов
2. Блойчейн и распределенные системы как симплициальные комплексы и их пропускная способность как фундаментальная группа
3. Теоретическая физика, E8 и слоения Хопфа
4. Инфинити категории и теория струн

А также сугубо философские модели в качестве дополнения к диссертации (все-таки доктор философии должен уметь чуть больше чем просто в математику):

1. Формализация мадхьямики и четырех благородных истин
2. Формализация эзотеорических систем и моделей сознания

Тут есть уже как минимум два автора которые основали это течение и есть на кого сослаться.

Предпучковая теория типов без категорий, на моноидах для наглядности

Читал про вселенные, дошел до треда с @akuklev 2014 года :-) http://math.andrej.com/2014/01/13/univalent-foundations-subsume-classical-mathematics/

В рамках концепции "не держи в себе хуйню", я решил создать новый суперпопулярный канал "Формальная Философия". Пока там один подписчик, но всё в ваших руках. Когда будет 100, начну постить код на кубике туда. Здесь же будет только BDSM. Чмоге, t.me/formalphilosophy