TN
Size: a a a
2018 May 21
Для любителей монад у меня есть хорошая новость, самое последнее расширение HoTT, cohesivett, или модальная теория типов, которая синтаксически хачит такие штуки как линейность, окресности, связность, бесконечно малые и шейпы как фундаментальные инфинити групоиды. Там три вида контекстов Γ | ∆ | Ξ. И 6 операций — cohesive модалити ʃ (групоид, комонада) ⊣ ♭ (комонада, дискретность) ⊣ ♯ (монада, кодискр.) и дифференциальные модалити ℜ (редукции, комонада, гладкость) ⊣ ℑ (бесконечно малые фиг. модальности, étale морфизмы, монада) ⊣ & (комонада).
2018 May 22
TN
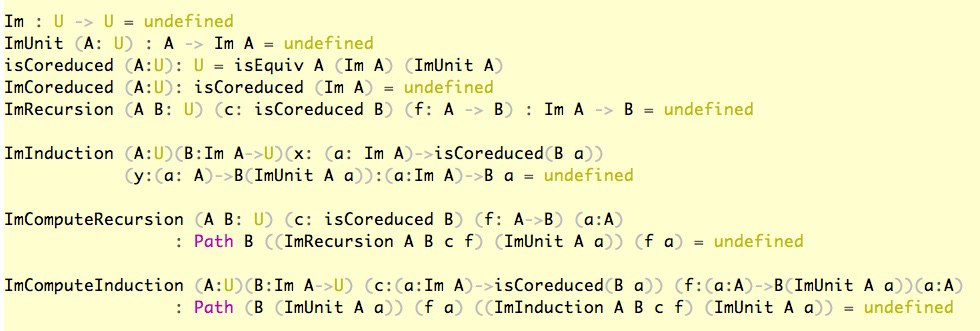
Модальная теория типов. Загнали акиомы и погнали. Невозможно же посчитать бесконечно малые. Можно сюда алгоритмы вставить которые будут комонадично считать до определенной точности или в тайпчекер зашить! Тут записано https://ncatlab.org/nlab/show/infinitesimal+shape+modality коредуцированные объекты.
2018 May 27
TN
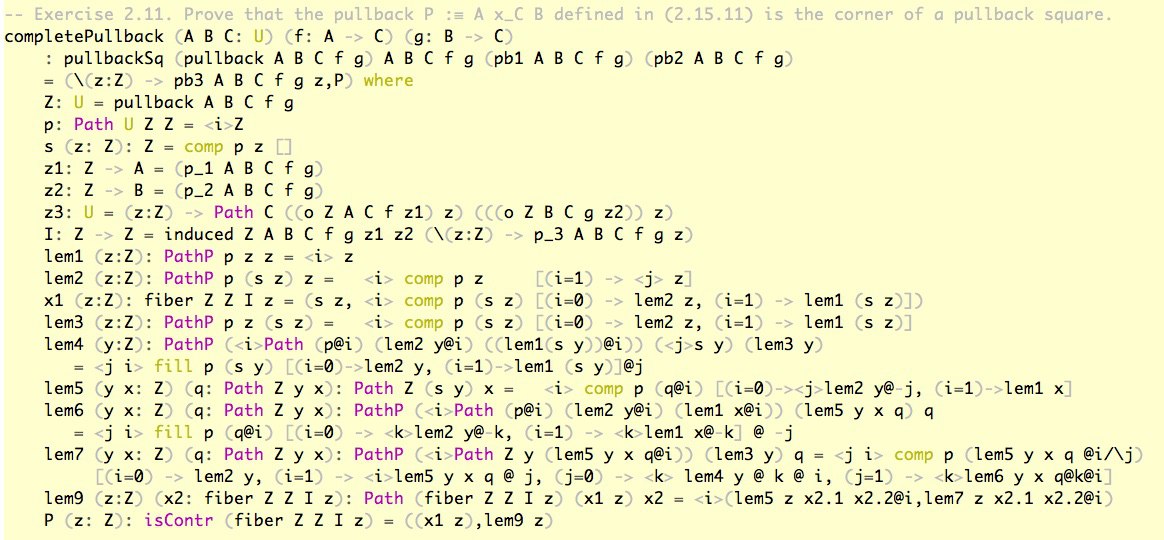
Как известно понять теорию категорий можно только если научился строить лимиты, а понять теорию гомотопий можно, если научился строить гомотопические лимиты! Гомотопический лимит в общем случае не равен категорному. Определение лимита простое — для любых f: A -> C и g: B -> C это ∑ (a: A) ∑ (b: B) [ f(a) =C f(b) ] . Т.е. гомотопический лимит это обобщение расслоения. Кроме Кубической Теории Типов есть еще и Кубическая Гомотопическая теория, в которй 0-клетки — это пространства, 1-клетки — это расслоения, 2-клетки — это лимиты и колимиты, и т.д. В учебнике HoTT троллят читателя и вместо того, чтобы дать пулбеки и пушауты главами, пулбек предлагают решить как упражнение 2.11 ко второй главе.
TN
Чтобы определить гомотопический колимит или пушаут, уже недостаточно пи и сигмы даже чтобы записать сигнатуру, нужны либо высшие индуктивные типы, либо, если вы умеете (а я вам рассказывал), ипредикативную кодировку. Проще говоря, нужно умножение в лимите заменить на сумму. Покажем как выглядит гомотопический колимит, это для функций f: C -> A, g: C -> B по сути сумма типов po1: A -> colim, po2: B -> colim и их равенства po3: (c: C) -> po1 (f c) = po2 (g c). Нужно построить для этого типа рекурсор и индукцию, кто возьмется?
TN
TL;DR Первая лекция. Формальная модель MLTT путем прямого встраивания в теорию типов
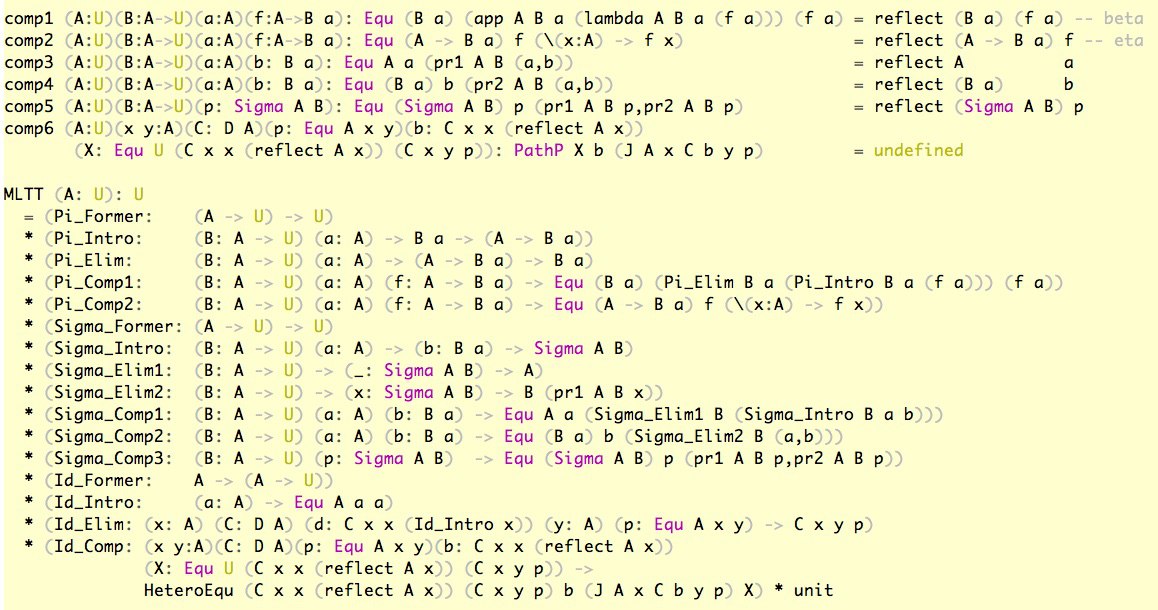
Стрим на мокуме начинается с "Конструктивного доказательства унивалентности", теоремы которая стала возможной только в августе 2017 года! Я думаю надо понижать планку и рассказать вам о первой лекции, которую я всегда даю по завтиповой теории. В этой лекции мы формально выписываем все формейшин рулы, интродакшин рулы, элиминейшин рулы и бета и эта равенства для трех типов, из которых состоит MLTT: Пи, Сигма и Равенство. И что интересно, если записать MLTT на самой MLTT то, получится, что доказательство большинства равенств будет состоять из reflection интродакшин рула от типа равенства. Таким образом показывается, что NBE настолько мощная штука, что может доказать почти все теоремы MLTT, кроме компютейшинал правила (эта-правило) для равенства. Я засекал на видосе live-кодинг и формального доказательства всей MLTT в кубике у меня уместилось в пару часов. В качестве пейпера который можно взять как основу для данной демонстрации я беру Мартина Хоффмана и Томаса Страйхера "Групоидная интерпретация теории типов", работы с которой начался путь в унивалентные основания.
Стрим на мокуме начинается с "Конструктивного доказательства унивалентности", теоремы которая стала возможной только в августе 2017 года! Я думаю надо понижать планку и рассказать вам о первой лекции, которую я всегда даю по завтиповой теории. В этой лекции мы формально выписываем все формейшин рулы, интродакшин рулы, элиминейшин рулы и бета и эта равенства для трех типов, из которых состоит MLTT: Пи, Сигма и Равенство. И что интересно, если записать MLTT на самой MLTT то, получится, что доказательство большинства равенств будет состоять из reflection интродакшин рула от типа равенства. Таким образом показывается, что NBE настолько мощная штука, что может доказать почти все теоремы MLTT, кроме компютейшинал правила (эта-правило) для равенства. Я засекал на видосе live-кодинг и формального доказательства всей MLTT в кубике у меня уместилось в пару часов. В качестве пейпера который можно взять как основу для данной демонстрации я беру Мартина Хоффмана и Томаса Страйхера "Групоидная интерпретация теории типов", работы с которой начался путь в унивалентные основания.
TN
NOTE: На самом деле в MLTT формально еще присутствуют Nat, List и W-типы, но поскольку мы знаем, что такое черч-кодировка, то мы можем закодировать эти типы через пи и сигму, так что вообщем-то они для нас всего-лишь аксиомы, а не примитивы тайп чекера. С другой стороны Nat, List и W никто в тайпчекер не включает, а сразу уже индуктивные семейства типов, привычые нам data и codata. Способов кодировок я знаю минимум шесть!
2018 May 29
TN
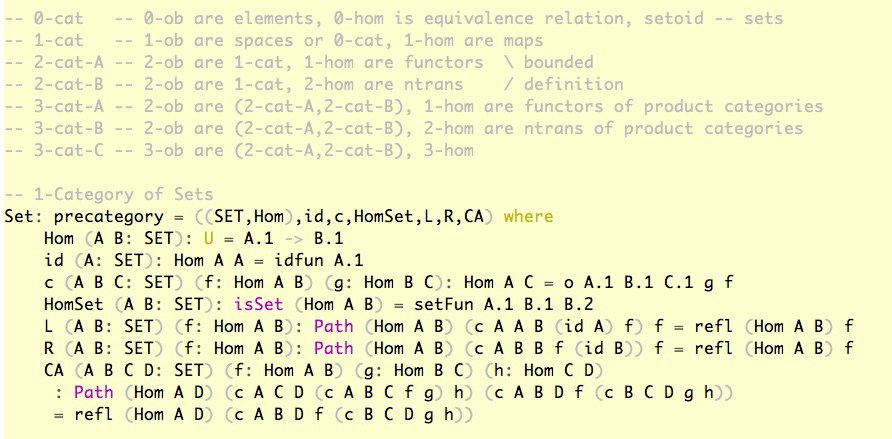
Урок Второй. Построение категорий от Set до Инфинити!
После первой 2-часовой лекции по MLTT, где детально разбираются Пи, Сигма, Путь и все их компоненты Formation/Inro/Elim/Rec/Case/Induction/Eta/Beta (а у Пути еще дополнительных куча subst, trans, все конечно через J выражаются, но через J реально никто не пишет, поэтому надо учить сразу культурке). У Пи типа есть еще funExt аксиома без которой не доказывается, что тип морфизмов является множеством, поэтому конструктивное построение инфинити категорий было невозможно до agda --cubical. Если морфизмы образуют не множество, а групоид, то это уже будет другая категория и так дальше до инфинити групоида. Кроме этого категории еще вкладываются друг в друга, например 0-категория — это множества или сетоид, где отношение Hom A B — это отношение эквивалентности на множествах, 1-категория, это категория где объекты — это 0-категории, множества или топологические пространства, а морфизмы — это отображения, в 2-категориях объекты — это 1-категории или просто категории, 1-морфизмы — это функторы, а 2-морфизмы — это естественные преобразования. На втором уроке можно уже строить категорию Множеств. Ну а категорию функторов можно давать уже после полного введения в теорию категори с лимитами. И уже только после теорката и категории функторов можно прееходить к семантике зависимой теории, категории контекстов, где морфизмы — это подстановки и категориям с семействами. Только сейчас решил написать это.
После первой 2-часовой лекции по MLTT, где детально разбираются Пи, Сигма, Путь и все их компоненты Formation/Inro/Elim/Rec/Case/Induction/Eta/Beta (а у Пути еще дополнительных куча subst, trans, все конечно через J выражаются, но через J реально никто не пишет, поэтому надо учить сразу культурке). У Пи типа есть еще funExt аксиома без которой не доказывается, что тип морфизмов является множеством, поэтому конструктивное построение инфинити категорий было невозможно до agda --cubical. Если морфизмы образуют не множество, а групоид, то это уже будет другая категория и так дальше до инфинити групоида. Кроме этого категории еще вкладываются друг в друга, например 0-категория — это множества или сетоид, где отношение Hom A B — это отношение эквивалентности на множествах, 1-категория, это категория где объекты — это 0-категории, множества или топологические пространства, а морфизмы — это отображения, в 2-категориях объекты — это 1-категории или просто категории, 1-морфизмы — это функторы, а 2-морфизмы — это естественные преобразования. На втором уроке можно уже строить категорию Множеств. Ну а категорию функторов можно давать уже после полного введения в теорию категори с лимитами. И уже только после теорката и категории функторов можно прееходить к семантике зависимой теории, категории контекстов, где морфизмы — это подстановки и категориям с семействами. Только сейчас решил написать это.
TN
Почему категорию множеств можно давать сразу на втором уроке без теорката? Потому, что в доказательствах свойств категории испольется только refl, такой же фокус как и с инференс правилами встроенной теории типов (самодоказательство, пруф чекинг тайп чекера по сути). Остается только детально разбрать доказательствао setFun которое говорит, что если кодомен множество, то стрелка тоже множество, ну а у нас не только кодомен множество, но и домен, так что доказательство тоже тривиальное, и как раз оно требует funExt.
TN
Сама структура SET тоже непростая, и для общей реализации надо использовать n-groupoid, так как isSet предикат в SET = (X: U) * isSet X — это 0-групоид. Благо это все можно рассказать на первом уроке.
TN
Объектами 3-категория будет 2-тапл 2-категорий и дальше по индукции. Просто начиная с 4-категории уже начинает резко нехватать бумаги из-за симплициальной струтктуры инфинити категорий, и непонятно, кому и зачем это может понадобиться.
TN
Думаю можно написать генератор сигнатур для инфинити категорий. Но только через метапрограммирование, напрямую AST генерировать, эффективнее всего. Вот например башня из трех сигнатур по которой все понятно:
TN
1-hom (C D: cat): U — сигнатура функтора
2-hom (C D: cat) (F G: 1-hom C D): U — сигнатура естественного преобразования
3-hom (C D: cat) (F G: 1-hom C D) (I J: 2-hom C D F G): U — сигнатура 3-морфизма
Для любителей матфизики, введение в n-категории Джона Баеза: http://math.ucr.edu/home/baez/ncat.ps
2-hom (C D: cat) (F G: 1-hom C D): U — сигнатура естественного преобразования
3-hom (C D: cat) (F G: 1-hom C D) (I J: 2-hom C D F G): U — сигнатура 3-морфизма
Для любителей матфизики, введение в n-категории Джона Баеза: http://math.ucr.edu/home/baez/ncat.ps