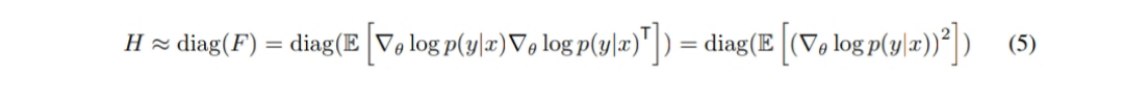MО
Size: a a a
2021 June 30
Фурье применяют для свертки. А тут где вы свертку разглядели? Вот ели у вас не просто горка, а полупрозрачна тогда что бы собрать все прозрачные слои в один можно и Фурье использовать. Но вместо прямого алгоритма за O(n) получите за O(nLog(n))
T
Да я хотел просто гауссово распределение через Фурье прогнать, получить "ступеньки" и с помощью них построить горку
MО
Я не возражаю. Однако на напоминаю.
MО
В сумасшедшем доме ссорятся бывшие студенты ФИЗТЕХа. Первый:
- Да я, тебя, сейчас продифференцирую!
- Не сможешь!
- Тогда я, тебя, проинтегрирую!!
- Нет! Не сможешь!!
- Почему-у-у!?!?!?
- Потому, что Я "е" в степени икс!!!!
- Да я, тебя, сейчас продифференцирую!
- Не сможешь!
- Тогда я, тебя, проинтегрирую!!
- Нет! Не сможешь!!
- Почему-у-у!?!?!?
- Потому, что Я "е" в степени икс!!!!
T
Справедливо. Может есть более изящный способ нарисовать?
MО
Так взять гаусиану и нарисовать без интеграла Фурье просто дискретизировать с нужным шагом.
T
Дык Фурье и используется в дискретизации
MО
Нет дискретизация это просто перевод из гладкой функции в набор отсчетов. Для 2-х мерного случая это просто два цикла.
for x:=-n/2 to n/2 step 1 do
for y:=-m/2 to m/2 step 1 do
M[x,y]:=Gaus(x,y);MО
Для двухмерного случая. Ядра по x и y перемножаются.
Gaus(x,y):=1/(2*Pi*s^2)*exp(-(x^2+y^2)/(2*s^2))
s-сигма средне квадратичное отклонение.
Ядро имеет размер -r, ..., -1,0, 1,..,r
N=2*r+1
Из правила трех сигм имеем взаимосвязь размера ядра и сигмы N=3*s. r=(N+1)/2=s*3/2+0.5 Более точная взаимосвязь такая
r:=floor(s * 3*sqrt(2*pi)/4 + 0.5);
Gaus(x,y):=1/(2*Pi*s^2)*exp(-(x^2+y^2)/(2*s^2))
s-сигма средне квадратичное отклонение.
Ядро имеет размер -r, ..., -1,0, 1,..,r
N=2*r+1
Из правила трех сигм имеем взаимосвязь размера ядра и сигмы N=3*s. r=(N+1)/2=s*3/2+0.5 Более точная взаимосвязь такая
r:=floor(s * 3*sqrt(2*pi)/4 + 0.5);
2021 July 14
B
У меня возникла небольшая идея (не для вас, простите), но для неё мне нужны ответы от математиков или связанных с этим специалистов. Что, как вы думаете, такое математика? Чем она занимается? Понимаю, что вопросы звучат глупо, но что поделать.
Простите за то, как это выглядит.
Простите за то, как это выглядит.
IP
Определение и подробности из Википедии вполне корректны, советую ознакомиться.
2021 July 15
MО
Математика это умение жанглировать формулами.
2021 July 22
V🇺
Господа, а бывают ли какие-то методы посчитать(/аппроксимировать) след гессиана функции быстрее чем за квадрат от числа переменных?
V🇺
а, вот такое нашел http://www.cs.tau.ac.il/~stoledo/Bib/Pubs/trace3.pdf
EZ
Лапласиан типа?
V🇺
EZ
Хотя хз насколько это хорошо именно для трейса
V🇺
это что-то из natural gradient?
EZ
Кажется нет, просто диагональ матрицы Фишера аппроксимирует гессиан