А вообще, я ж детЯм рассказываю штуки абстрактные, вообще на твиче. Играем в математику. Вон на прошлом стриме гуляли по 4D аж четыре часа. Ничего все выжили, в хорошем настроении

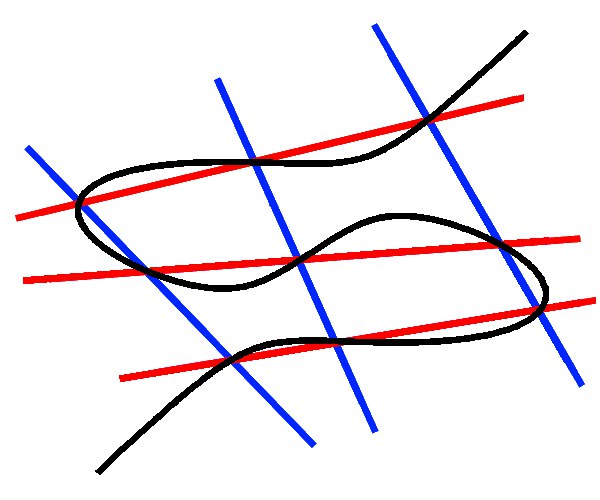
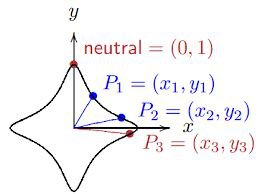
На самом деле Сонг дает магические рецепты, а не объяснения. Например, из его построения видно, что операция комутативна: A+B = B+A (ведь если точки А и B поменять местами - они дадут ту же прямую). Комутативность групповой операции объясняет, почему для неё используют знак +, а не более привычное для групп умножение (группа-то Абелева). Но из его построения вообще не следует гораздо более важноe свойство заданной операции, а именно - что она - ассоциативна (A+B)+C=A+(B+C). Я как-то после Ханибеджера спросил Сонга, почему он не рассказывает теорему о 9-ти точках на кубической кривой, оказалось - он её не знал. А это ведь центральный элемент в построеннии групповой операции на эллиптических кривых.  

https://ru.m.wikipedia.org/wiki/Теорема_о_девяти_точках_на_кубической_кривой

Во-первых эта теорема делает очевидной ассоциативнлсть, а во вторых из этой теоремы следует, что та точка, которую мы берем за 0 - действительно должна лежать на кривой, причем выбрать её можно произвольно, в любом месте. Если провести через такой 0 прямую, и она пересечет кривую в двух точках, то такие точки будут считаться обратными друг другу. Т.е. не обязательно вертикально отражать. Это - частный случай. А вот почему, при чем тут бесконечность и вертикальное отражение - это другой вопрос. Дело в том, что «усы» нашей элиптической кривой растут настолько быстро, что если начать двигать точку «нуля» вправо вверх неограниченно по такому усу, то прямая, соединяющая любую конечную точку с таким убегающим «нулём» будет стремиться к вертикали, и действительно имеет предел как вертикальная линия. Это кажется странным, ведь вроде по оси икс «нуль» уехал бескончно вправо, но и по оси игрек он уехал бесконечно вверх причем «быстрее» чем по оси икс, таким образом наклон секущей стал вертикальным. И ведь такой наклон в практических вычислениях использовать гораздо сподручнее, (чем любой другой) ибо здесь просто можно сменить знак у игрек-координаты и всё (в кончных полях - взять обратный по сложению элемент). Поэтому и загоняют эллиптический «нуль» в бесконечность. И он действительно лежит на кривой... как-то так.  Если наврал @khovratovich поправит, ну или в любом случае расскажет как правильно в своей лекции... -)

Сейчас Дима Ховратович кинет в меня тапком (символом Лежандра и квадратичными вычетами) - но по большому счёту, можно даже взять просто кружочек - кольцо вычетов по простому модулю. И делать всю криптографию там. Горааааздо боле наглядная группа чем эллиптические кривые.

Кстати, мне кажется в мейнстримной айти движухе есть ощущение не "бетховены перамида" а что-то типа "вы там все космонавты в своем этом блохчейне, не хочу иметь дел"

90% этих айтишников до сих пор думают, что доллар подкреплён золотом

Кстати насчет хэшей и постквантовой криптографии можно было бы подкаст сделать и я даже знаю кого туда позвать - Рому Олейника

Вобщем точно с меня теперь что-то для ББ

Кек, я оказывается тоже там)
Дудь ок, мне не зашло - но хорошо если кому-то понравилось.

За женщин в видео я думаю норм было бы сказать - смотрите, в этом видео нет женщин, и в долине их тоже (почти) нет, на этом для меня бы вопрос был закрыт.